Sind die folgenden Funktionen auf ihrem gesamten Definitionsbereich stetig?

Question

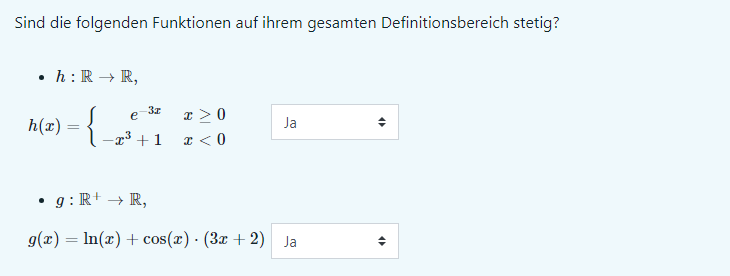
Bei h(x) sind die Funktionen stetig und es gibt keine Sprungstellen, deshalb insgesamt stetig.

Bei g(x) sind die Funktionen ln(x), cos(x) und 3x+2 stetig und daher sind sie auch bei Addition und Multiplikation stetig.

Das sind die Gründe, warum ich auf "Ja" geantwortet habe.

Ich wollte wissen, ob meine Überlegungen und Antworten richtig sind ?

Vielen Dank im Voraus

Answer 1

Ja, stimmt alles, und gut, dass Du Begründungen formuliert hast. Bei g hast Du hoffentlich auch den Defbereich von ln geprüft (es muss ja alles definiert sein). Bei h solltest Du noch genauer sagen, warum keine Sprungstelle vorliegt.

Comments

Genau bei g geht die Funktion von ℝ⁺ deshalb habe ich auf "Ja" geantwortet. Es gilt D⊆ℝ und D∈ℝ⁺ . Wenn sie aber mit gesamten Definitionsbereich D∈ℝ meinen, dann ist g nicht stetig , weil für x<0 ja ln nicht definiert ist ?

---

Es ist \( D= \mathbb{R}^+ \). Steht aber da.

---

Nein, alles ok, denn hier wurde ja für \(g\) schon der Defbereich \(D=\R^+\) angegeben. Daher muss man nicht drüber nachdenken, ob er noch größer sein könnte.