Wie geht die Aufgabe

Question

Text erkannt:

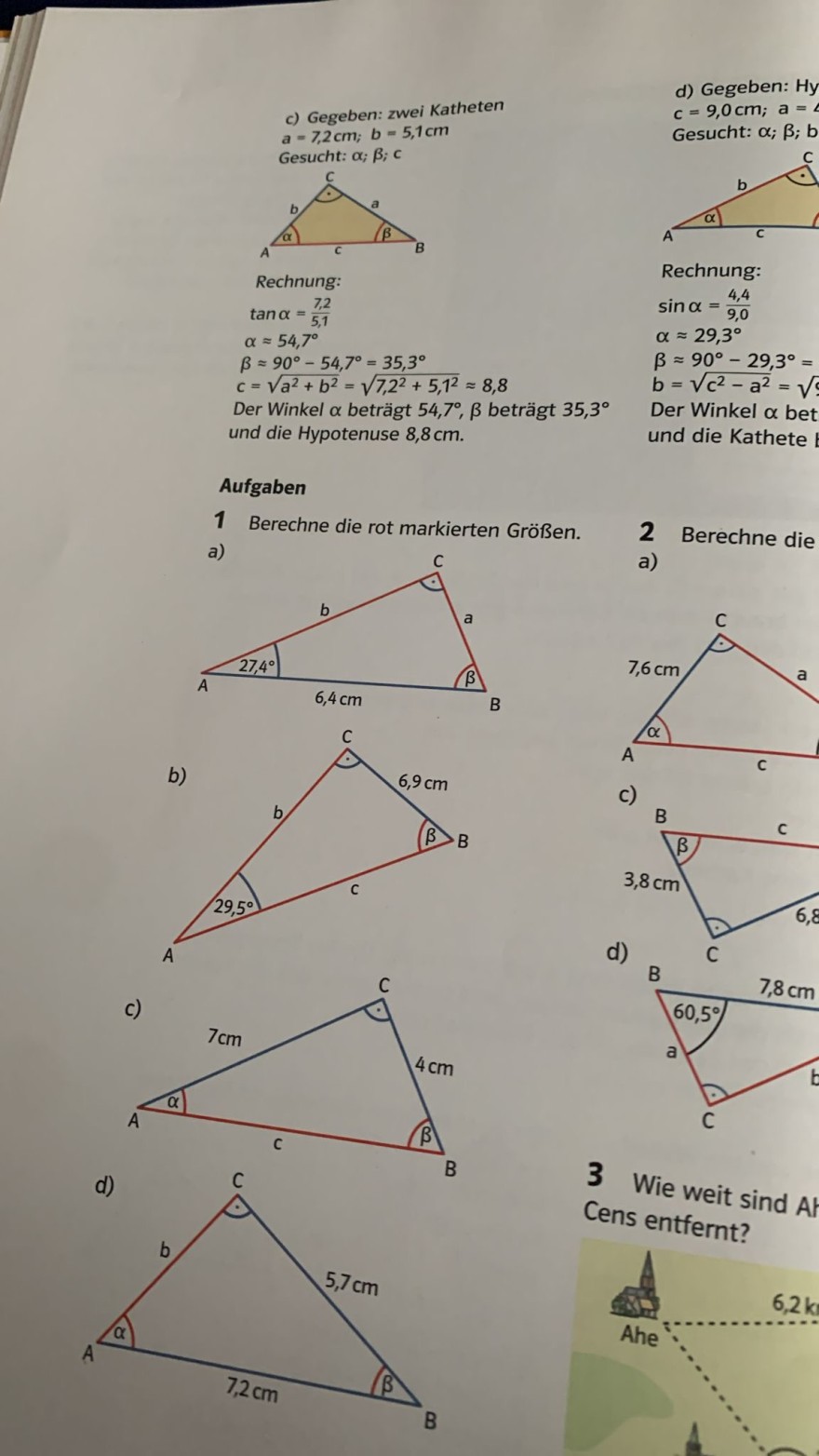
c) Gegeben: zwei Katheten
\( \boldsymbol{a}=7,2 \mathrm{~cm} ; \boldsymbol{b}=5,1 \mathrm{~cm} \)
Gesucht: \( \alpha ; \beta ; c \)

Rechnung:
\( \begin{array}{l} \tan \alpha=\frac{7,2}{5,1} \\ \alpha \approx 54,7^{\circ} \\ \beta \approx 90^{\circ}-54,7^{\circ}=35,3^{\circ} \\ c=\sqrt{a^{2}+b^{2}}=\sqrt{7,2^{2}+5,1^{2}} \approx 8,8 \end{array} \)

Der Winkel \( \alpha \) beträgt \( 54,7^{\circ}, \beta \) beträgt \( 35,3^{\circ} \) und die Hypotenuse \( 8,8 \mathrm{~cm} \).

Aufgaben
1 Berechne die rot markierten Größen.
a)
b)
c)
d)
d)
2 Berechne die a)
c)
\( \alpha \approx 29,3^{\circ} \)
\( \beta \approx 90^{\circ}-29,3^{\circ}= \)
\( b=\sqrt{c^{2}-a^{2}}=\sqrt{ } \)
Der Winkel \( \alpha \) bet und die Kathete
d) Gegeben: Hy
Gesucht: \( \alpha ; \beta \); b
Rechnung:
\( \begin{array}{l} \sin \alpha=\frac{4,4}{9,0} \\ \begin{array}{l} \alpha \approx 29,3^{\circ} \\ \beta \approx 90^{\circ}-29,3 \\ =\sqrt{c^{2}-a^{2}} \end{array} \\ \text { nd die Kathete } \end{array} \)
c

Aufgabe:

…

Problem/Ansatz:

Comments

Was hast du schon versucht? Dein Problem?

Poste nicht soviele Aufgaben auf einmal. Das schreckt Helfer ab.

Answer 1

Im rechtwinkligen Dreieck gilt für einen Innenwinkel φ:

\( sin φ= \frac{Gegenkathete.von.φ}{Hypotenuse} \)

\( cos φ= \frac{Ankathete.von.φ}{Hypotenuse} \)

\( tan φ= \frac{Gegenkathete.von.φ}{Ankathete.von.φ} \)

Als Gegenkathete bezeichnet man die Kathete, die φ gegenüberliegt.

Als Ankathete bezeichnet man die Kathete, die an φ anliegt.

Und wenn du von einem Dreieck außer dem rechten Winkel noch einen zweiten Winkel hast kannst du den dritten Innenwinkel direkt berechnen (alle drei Winkel ergeben zusammen 180°).