Lineare Abbildungen, Ungleichung mit Rangformel

Question

Aufgabe:Zeige/Widerlege folgende Aussage: für lineare Abbildungen \( \varphi : V_1 \rightarrow V_2 \) und \( \psi : V_2 \rightarrow V_3 \) gilt \( Rang(\psi \circ \varphi) \leq Rang(\psi) \)

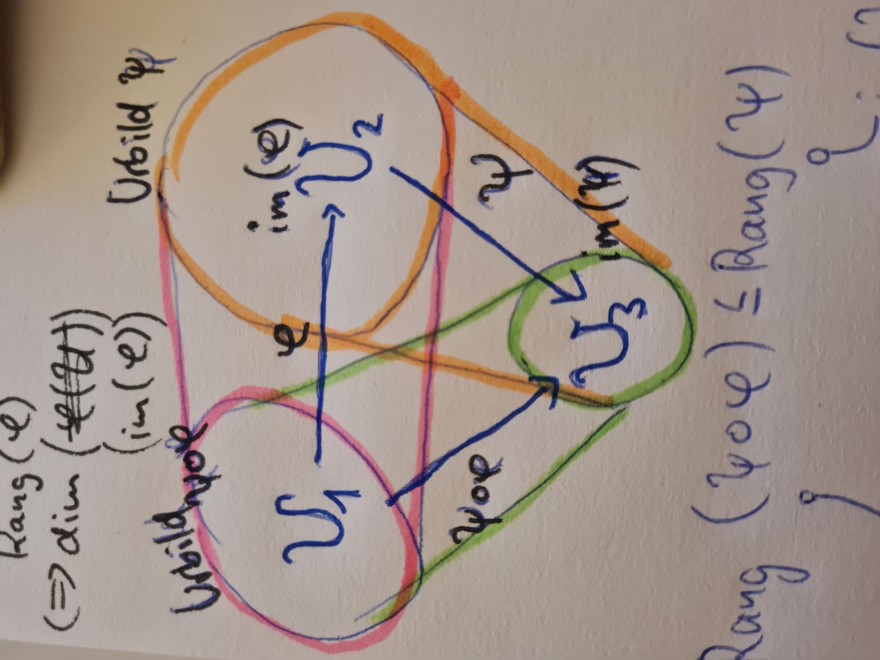
Problem/Ansatz: Aussage ist wahr, aber mein Ansatz sieht man in diesem Diagramm. Nun ich stehe auf dem Schlauch mit dem Zusammenhang zwischen Bild und Urbild. Die Kreise sollen einen größenunterschied zwischen Bild und dessen Urbild darstellen, damit die Ungleichung deutlicher wird. Jetzt fällt mir aber noch was anderes auf, denn eigentlich sollte mein Kreis um \( U_1 \) am größten sein, oder nicht?Bitte um eure Hilfe.

Text erkannt:

\( \operatorname{Rang}(\psi \circ \varphi) \leqslant \operatorname{Rang}(\psi) \)

Text erkannt:

\( \operatorname{Rang}(\psi \circ \varphi) \leqslant \operatorname{Rang}(\psi) \)

Text erkannt:

\( \operatorname{Rang}(\psi \circ \varphi) \leqslant \operatorname{Rang}(

Answer 1

Sei \(v_3\in \operatorname{Bild} \psi\).

Sei \(v_2\in V_2\) mit \(\psi(v_2)=v_3\).

Angenommen \(v_2 \in \operatorname{Bild} \varphi\). Dann ist \(v_3\in \operatorname{Bild} \psi \circ\varphi\).

Also ist \(\operatorname{Bild} \psi \circ\varphi \subseteq \operatorname{Bild} \psi\).

Comments

Ok, nice danke oswald -> Rep+