Aufgabe:
Ist diese Ableitung der Lagrange Funktion richtig? Bin mir nicht sicher ob ich das richtig gemacht habe, komme nicht auf die Lösung von x1, x2 und λ, kann aber auch sein das ich es falsch löse. Könnte da jemand bitte drüber schauen, danke für jede Hilfe
Lagrange Funktion
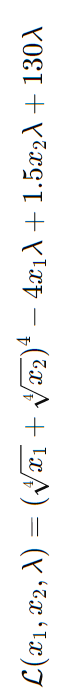
Text erkannt:
\( \mathcal{L}\left(x_{1}, x_{2}, \lambda\right)=\left(\sqrt[4]{x_{1}}+\sqrt[4]{x_{2}}\right)^{4}-4 x_{1} \lambda+1.5 x_{2} \lambda+130 \lambda \)
x1
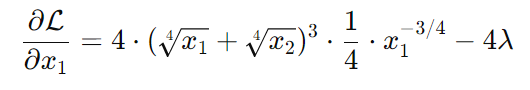
Text erkannt:
\( \frac{\partial \mathcal{L}}{\partial x_{1}}=4 \cdot\left(\sqrt[4]{x_{1}}+\sqrt[4]{x_{2}}\right)^{3} \cdot \frac{1}{4} \cdot x_{1}^{-3 / 4}-4 \lambda \)
x2
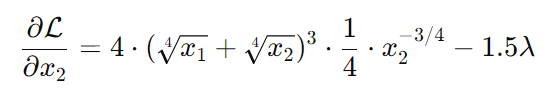
Text erkannt:
\( \frac{\partial \mathcal{L}}{\partial x_{2}}=4 \cdot\left(\sqrt[4]{x_{1}}+\sqrt[4]{x_{2}}\right)^{3} \cdot \frac{1}{4} \cdot x_{2}^{-3 / 4}-1.5 \lambda \)
λ
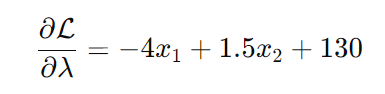
Text erkannt:
\( \frac{\partial \mathcal{L}}{\partial \lambda}=-4 x_{1}+1.5 x_{2}+130 \)