Aufgabe:
Ersetzt man die Platzhalter a und b in geeigneter Weise, so kann mit dem Term
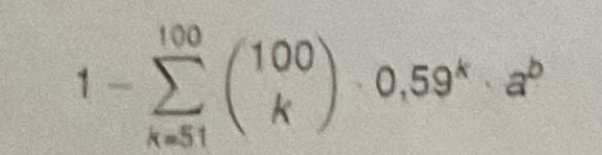
Text erkannt:
\( 1-\sum \limits_{k=51}^{100}\left(\begin{array}{c}100 \\ k\end{array}\right) \cdot 0,59^{k} \cdot a^{b} \)
die Wahrscheinlichkeit eines Ereignisses im Sachzusammenhang berechnet werden.
Geben Sie an, durch welche Zahlen die Platzhalter zu ersetzen sind, und beschreiben Sie das zugehörige Ereignis.
Problem/Ansatz:
für a^b habe ich 0,41^100-k ausgewählt
Sachzusammenhang: Max. 50% der Kunden haben Datenschutzbedenken