Hallo Johanna,
ich muss mich im Namen des gesamten Forums für die voreilig-oberflächlichen Antworten entschuldigen.
ZUERST wäre zu klären, welcher der beiden folgenden Fälle vorliegt:
(1) Der Ball klemmt an der Kegelinnenwand fest (nur diesen Fall haben die bisherigen Antwortgeber als gegeben angenommen)
oder
(2) Der Ball ist so klein (bzw. der Durchmesser des unteren Zylinders mit 2 cm so groß), dass der Ball nicht an den Zylinderwänden klemmt, sondern auf dem Kreis des Ausflusszylinders einfach nur aufsitzt.
Hier
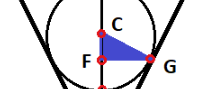
wäre vorab (wenigstens zeichnerisch) zu prüfen, ob FG ≥ 1cm oder FG < 1cm ist.