Wie bestimme ich die Schnittpunkte zweier Funktionen wenn ein Bruch dabei ist?

Question

Aufgabe:

Bestimmen Sie die Schnittpunkte der Funktion f(x) mit g(x) = 2x - 2.

Problem/Ansatz:

\( f(x)=\frac{x^{2}-8 x+4}{2 x+2} \)

Comments

Vom Duplikat:

Titel: Wie bestimme ich die Schnittpunkte der Funktion f(x) mit g(x)?

Stichworte: funktion,schnittpunkte

Aufgabe:

Bestimmen Sie die Schnittpunkte der Funktion f(x) mit g(x) = 2x - 2.

Problem/Ansatz:

\( f(x)=\frac{x^{2}-8 x+4}{2 x+2} \)

Answer 1

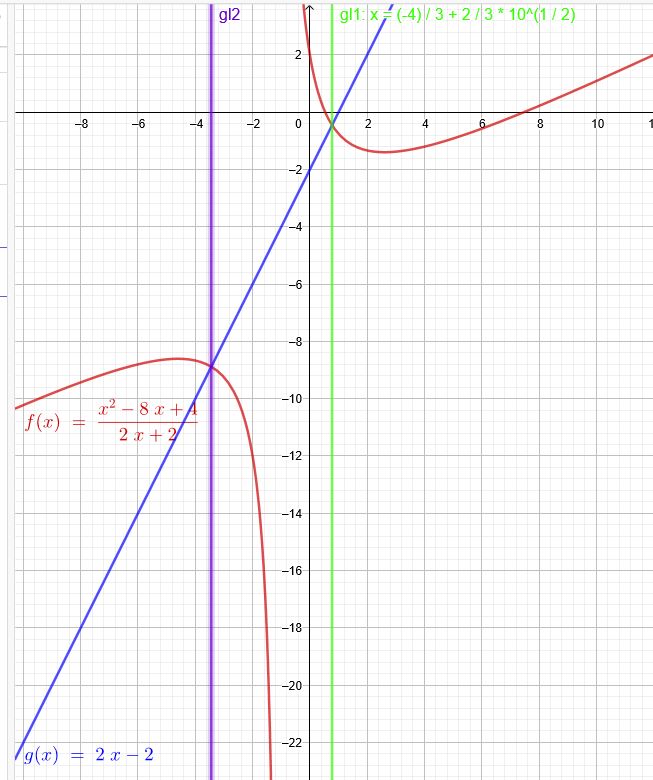
\( f(x)=\frac{x^{2}-8 x+4}{2 x+2} \)   mit \(x≠-1\)    \(g(x) = 2x - 2\)   

\( \frac{x^{2}-8 x+4}{2 x+2}=2x - 2|\cdot(2x+2 )\)

\( x^{2}-8 x+4=(2x - 2)\cdot(2x+2 )=4x^2-4\) wegen 3.Binom

\( x^{2}-8 x=4x^2-8\) Seitentausch

\( 4x^2-8=x^{2}-8 x\)

\( 3x^2+8x=8|:3\)

\( x^2+\frac{8}{3}x=\frac{8}{3}\) quadratische Ergänzung:

\( x^2+\frac{8}{3}x+(\frac{4}{3})^2=\frac{8}{3}+(\frac{4}{3})^2=\frac{8}{3}+\frac{16}{9}\)  1.Binom:

\( (x+\frac{4}{3})^2=\frac{40}{9}|±\sqrt{~~}\)

1.)

\( x+\frac{4}{3}=\frac{2}{3}\sqrt{10}\)

\(x_1=-\frac{4}{3}+\frac{2}{3}\sqrt{10}\)

2.)

\( x+\frac{4}{3}=-\frac{2}{3}\sqrt{10}\)

\(x_2=-\frac{4}{3}-\frac{2}{3}\sqrt{10}\)

Comments

Vielen Dank.

Wäre es also falsch wenn ich die zweite binomische Formel anwende?

Muss es unbedingt die dritte sein?

---

(2x - 2)·(2x +2) = 4x²-4 ist doch die dritte!!

Answer 2

Hi,

Ob da ein Bruch dabei ist oder nicht, ändert am Ansatz erstmal nichts. Setze die beiden Funktionen gleich:

$$2x-2 = \frac{x^2-8x+4}{2x+2}$$

Starte mit der Multiplikation des Nenners, dann ist der schonmal kein Problem mehr.

Du kommst klar?

Zur Kontrolle:

$$x_{1,2} = -\frac43\pm\frac{2\sqrt{10}}{3}$$

(Bist Du sicher beide Funktionen richtig abgeschrieben zu haben? Das Ergebnis ist unüblich krumm ;))

Die y-Werte bestimmst Du dann mit Einsetzen in einer der Funktionen.

Grüße

Answer 3

Gleichsetzen:

für x≠ -1:

(x^2-8x+4)/(2x+2) = 2x-2

x^2-8x+4=(2x-2)(2x+2) = 4x^2-4 (3. binom. Formel)

-3x^2-8x+8 = 0

Mitternachtsformel anwenden

oder:

x^2+(8/3)*x-8/3 =0

pq-Formel anwenden

Comments

Text erkannt:

\( \begin{array}{l} f(x)=\frac{x^{2}-3 x}{2 x+2} \quad g(x)=2 x+2 \\ f(x)=g(x) \\ \left.\frac{x^{2}-3 x}{2 x+2}=2 x+2 \quad \right\rvert\, \cdot 2 x+2 \\ x^{2}-3 x=2 x+2(2 x+2) \\ x^{2}-3 x=2 x+4 x+4 \\ x^{2}-3 x=6 x+4 \\ 1-6 x \\ x^{2}-9 x=4 \\ 1-4 \\ x^{2}-9 x-4=0 \quad \rightarrow p q \text {-Formel } \\ x_{1 / 2}=\frac{9}{2} \pm \sqrt{\left(-\frac{9}{2}\right)^{2}+4} \\ x_{1 / 2}=4,5 \pm \sqrt{24,25} \\ x_{1}=4,5+4,92=9,42 \\ x_{2}=4,5-4,92=-0,42 \\ S_{x_{1}}(9,42 / 20,84) \\ 5_{y_{2}}(-0,42 / 1,16) \end{array} \)

Kannst du bitte schauen ob das so stimmt. Also vom Prinzip her.

---

Wenn Du mit dem Nenner multiplizierst, dann setze um jede Seite eine Klammer. Dann passiert Dir Dein Fehler nicht, dass Du rechts die Klammer vergessen hast. Wenn man es ausführlich aufschreiben würde, sieht das so aus:

$$\frac{x^2-3x}{2x+2} = 2x-2 \quad|\cdot (2x+2)$$

$$\left(\frac{x^2-3x}{2x+2}\right)\cdot (2x+2) = \left(2x-2\right)\cdot (2x+2)$$

$$x^2-3x = 4x^2-4$$

Dabei wurde auf dem letzten Schritt rechts die dritte binomische Formel erkannt.

(Das heißt in Deinem korrigierten g(x) = 2x+2 müsste man die erste binomische Formel einsetzen). Das bekommst Du selbst hin?

Also unbedingt merken: Immer Klammern setzen!