Bedingung für Parameter d angeben, sodass Gerade eine Tangente zum Kreis ist?

Question

Aufgabe:

Folgende Aufgabe: Gegeben ist der

Kreis k: (x+3)² + (y-4)² =18 und die Gerade g: y=x+d

Ich soll eine eine Bedingung für den Parameter d angeben, sodass eine g eine Tangente ist.

Problem/Ansatz:

Ich weiß, dass der Abstand vom Kreismittelpunkt dem Radius entsprechen muss, deswegen habe ich gerechnet 18+3² +2² =43 und dachte deswegen, d muss 43 sein.

Im Lösungsheft steht d=1 oder d=13

Comments

Hallo,

(x+3)^2 + (y-2)^2 =18

(x+3)^2 + (x+d-2)^2 =18

x= ...

Diskriminante gleich Null setzen (Warum wohl?)

d=-1 oder d=11

:-)

---

sorry aber was ist hier die diskriminante?

---

okay also kommt dann heraus wenn ich es ausmultipliziere:

x²+6x+9+x²+d²+4=18

bin leider gerade etwas verwirrt, warum genau soll ich das d gleich 0 setzen ?

aber wenn ich das d =0 setze fällt es ja komplett weg, wie kann ich dann noch ausrechnen dass es -1 oder 11 ist? Kannst du mir bitte deine Rechnung dazu zeigen?

---

Hallo Eva,

mit (y-4)² :

(x+3)^2 + (x+d-4)^2 =18

x²+6x+9+x²+2x(d-4)+(d-4)²=18

Das ist eine quadratische Gleichung für x.

2x²+(-2+2d)x+(d²-8d+7)=0

x²+(-1+d)x+(0.5d²-4d+3.5)=0

x=(0.5-0.5d)±√(0.25-0.5d+0.25d²-0.5d²+4d-3.5)

x=(0.5-0.5d)±√(-0.25d²+3.5d-3.25)

Die Diskriminante steht unter der Wurzel.

Ist sie gleich Null, so gibt es genau einen Punkt, den Kreis und Gerade gemeinsam haben. Die Gerade ist dann eine Tangente.

-0.25d²+3.5d-3.25=0  |•(-4)

d²-14d+13=0

d=7±√(49-13)

d=1 oder d=13

:-)

Answer 1

Sind die Angaben korrekt? Bei diesem Kreis sollte  -1 und 11 herauskommen.

Du kennst die Steigung der Tangente. Nun mußt Du nur noch berechnen, wo der Kreis dieselbe Steigung hat. Dann kennst Du die Punkte.

Deine Rechnung macht für mich keinen Sinn.

Wie so oft hilft eine Skizze! Mach eine und stell sie ein.

Comments

\(d=-1\) oder \(d=11\) sollten die Parameter sein.

---

Ja genau, vertippt, danke,

---

habe leider falsch abgeschrieben. hab jetzt nochmal nachgeschaut es heißt eigentlich (y-4)²

Answer 2

Modelliere eine Gerade durch den Kreismittelpunkt die senkrecht zu den beiden Tangenten stehen soll. Ermittle die Schnittpunkte der Gerade mit dem Kreis und ermittle dann die Tangenten an den Kreis in diesen beiden Punkten.

Du kannst auch die Vektorrechnung benutzen um die Tangentenberührpunkte zu bestimmen. Dabei brauchst du auf der Geraden durch den Kreismittelpunkt ja nur den Radius entlang zum Kreisrand gehen und hast die beiden Punkte. Dann braucht man keine Gleichung lösen.

Das sieht wie folgt aus.

Comments

mir ist gerade aufgefallen, dass in der angabe steht (y-4)²=18 und nicht -2

tut mir leid mir unterlaufen leider öfter solche schlampigkeitsfehler

---

Ich habe meine Lösung etwas angepasst.

Answer 3

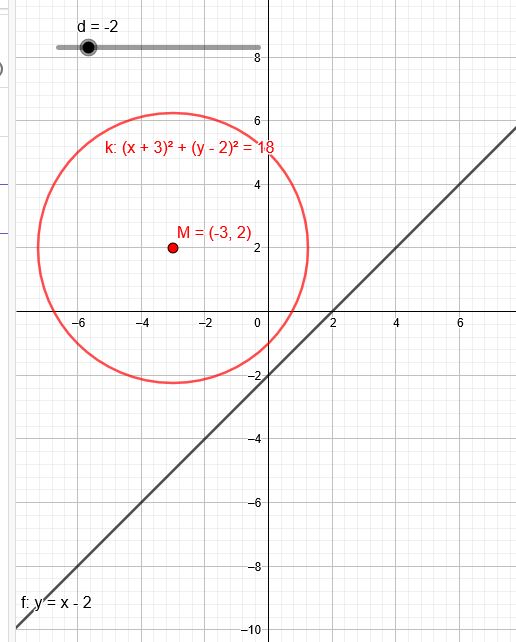
Die Orthogonale zu \(y=\red{1}x-2\) schneidet den Kreis

\((x+3)^2+(y-2)^2=18\) in den beiden Berührpunkten.

Die Steigung der ist \(m=-1\)

Die allgemeine Geradengleichung lautet \(y=mx+n\):

\(y=-\red{1}x+n\)

Der Mittelpunkt M\((\green{-3}|\blue{2})\) des Kreises liegt nun auf dieser Geraden:

\(\blue{2}=-\red{1}\cdot (\green{-3})+n\)

\(n=-1\)

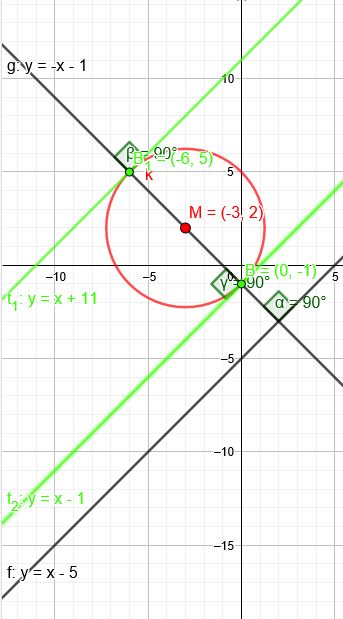
\(y=-x-1\)  Schnitt mit  \((x+3)^2+(y-2)^2=18\):

\((x+3)^2+(-x-1-2)^2=18\)

\((x+3)^2+(-x-3)^2=18\)

\(x_1=0\)       \(y(0)=-1\)

\(x_2=-6\)      \(y(0)=5\)

Kommst du nun alleine weiter?

Comments

danke für deine hilfe