Diverse Winkelberechnungsaufgaben Dreieck

Question

das könnte mir jemand mit diesen Aufgaben behilflich sein bitte. Wenn möglich mit einem übersichtlichem Lösungsweg.

Vielen Dank im Voraus.

Text erkannt:

Aufgabe 9
Gegeben sind die Winkel \( \alpha=45^{\circ} \) und \( \beta=20^{\circ} \). Berechnen Sie den Wínkel \( \gamma \).

Aufgabe 10
Gegeben sind die Winkel \( \alpha=25^{\circ} \) und \( \beta=55^{\circ} \).
Berechnen Sie die Winkel \( \gamma \) und \( \delta \).

Comments

Für das Verständnis ist es immer nützlich sich selber mal eine Skizze zu machen und versuchen allgemeine Abhängigkeiten zu entdecken.

Answer 1

Berechnen Sie den Wínkel \gamma .

Ich nehme an, Du willst das wissen, was Du in den Titel geschrieben hast.

Winkel ACM = alpha

Winkel CMA = 180° - 2 alpha = 90°

Winkel MCB = beta

Winkel BMC = 180° - 2 beta = 140°

gamma = 360° - 90° - 140° = 130°

Comments

Tut mir Leid für die Verwirrung, es ging mir um die ersichtliche Aufgabenstellung 8 & 9.

Der Titel war autogeneriert.

---

es ging mir um die ersichtliche Aufgabenstellung 8 & 9.

Ahso. Zwar wundere ich mich, weshalb Du dann 9 und 10 abgebildet hast, aber Du kannst davon ausgehen, dass bald jemand kommt und auch die zweite Aufgabe beantworten wird bzw. erklärt, warum dort gamma = 110° und delta = 65°. Bis dahin kannst Du es ja selber versuchen.

Answer 2

Aufgabe 10a)

Gegeben ist der Winkel \( \alpha=25^{\circ} \) .Berechnen Sie den Winkel  \( \delta \).

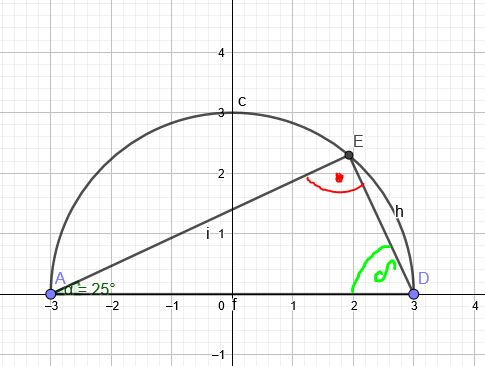
Das  Dreieck ADE hilft den Winkel \( \delta \) zu berechnen. Auf dem Thaleskreis beim Punkt E beträgt der Winkel immer eine Größe von \(90°\). Da die Winkelsumme im Dreieck \(180°\) ist, errechnet sich der Winkel bei D mit \( \delta=65° \)

10b) Gegeben ist der Winkel \( \beta=55^{\circ} \). Berechnen Sie den Winkel \( \gamma \).

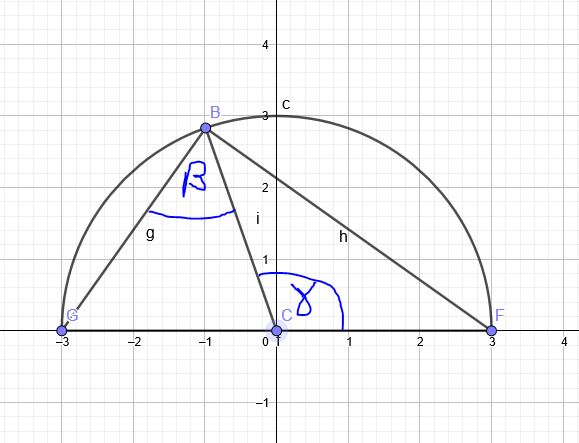
Das  Dreieck wird benötigt, um den Winkel bei C \( \gamma \) zu berechnen. Da der Winkel GBC \( \beta=55^{\circ} \) sein soll, muss nun der Winkel CBF \(90°- \beta=35°\)  sein. Der Winkel bei  F ist wegen der Gleichschenkligkeit des Dreiecks BCF auch \(35°\) groß.

Somit ist  \( \gamma=110° \)

Comments

Bitte korrigiere deine irreführende Geogebra-Datei.