Bestimme die Streckenverhältnisse b/a und c/b.

Question

Gegeben sind zwei zueinander senkrechte Geraden g und h, die sich in S schneiden. In einem Kreis K_c um S mit dem Radius c liegen fünf Kreise K_a mit dem Radius a. K_a1 hat den Mittelpunkt S. Die Mittelpunkte von K_a2 und K_a4 liegen auf g und die Kreise berühren K_c von innen. Die Mittelpunkte von K_a3 und K_a5 liegen auf h und die Kreise berühren K_c von innen. Vier Kreise K_b mit dem Radius b haben ihre Mittelpunkte auf g bzw. auf h. Alle vier Kreise K_b werden von K_a1 von innen berührt. Alle vier Kreise K_b berühren K_c von innen (siehe Abbildung). Bestimme b/a und c/b.

Answer 1

Nur mal meine Lösungen zum Vergleich.

b/a = √5/2 + 3/2 = Φ + 1 ≈ 2.618

c/b = √5/2 + 1/2 = Φ ≈ 1.618

Comments

Willst du noch Hinweise auf einen Lösungsweg geben?

---

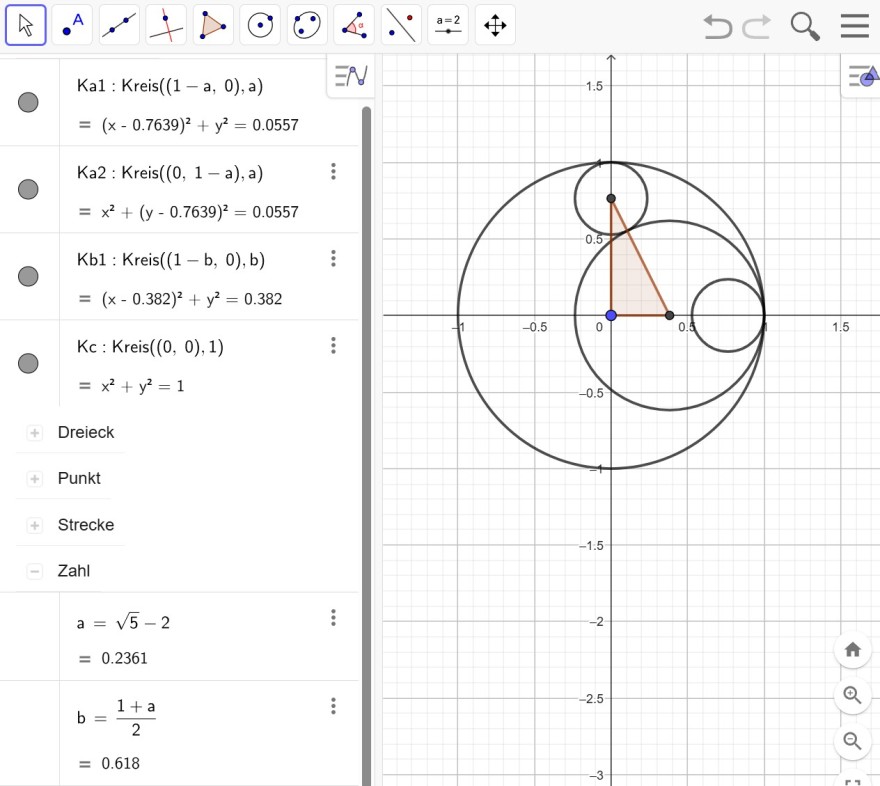
Ich habe zunächst definiert:

Kc hat den Mittelpunkt (0 | 0) und den Radius 1

Ka1 hat den Mittelpunkt (1 - a | 0) und den Radius a

Ka2 hat den Mittelpunkt (0 | 1 - a) und den Radius a

Kb1 hat den Mittelpunkt (1 - b | 0) und den Radius b

Da der Durchmesser von Kb sicher 1 + a ist ist der Radius b = (1 + a)/2

Das kann ich einsetzen

Kb1 hat den Mittelpunkt (1 - (1 + a)/2 | 0) und den Radius (1 + a)/2

Der Abstand der Mittelpunkte von Kb1 und Ka2 muss genau der Summe der beiden Radien a + b entsprechen. Mit dem Satz des Pythagoras also

(1 - a)^2 + (1 - (1 + a)/2)^2 = (a + (1 + a)/2)^2 --> a = √5 - 2

Der Rest ist dann recht einfach