Funktionenschar mit Steigungswinkel des Deichprofils

Question

Aufgabe:

Moderne Deiche werden mit einem möglichst flachen Gefälle auf der Flussseite konstruiert. Für den Steigungswinkel a des (flussseitigen) Deichprofils gegenüber der Horizontalen soll |a| ≤ 30° gelten. Berechnen Sie, für welchen Wert des Parameters k der Graph der Funktionenschar g_k die Bedingung |a| = 30° an der steilsten Stelle des (flussseitigen) Deichprofils erfüllt.

g_k(x) = k/1000*x*(x-25)²

Problem/Ansatz:

Ich kenne zwar die Lösung schon, weil ich sie mir durchgelesen habe, aber um ehrlich zu sein verstehe ich sie überhaupt nicht. Das man die Ableitung verwenden muss verstehe ich, weil die Ableitung die Steigung der Funktion an einer bestimmten Stelle gibt. Hier soll ja an der steilsten Stelle also den Wendepunkt überprüft werden. Aber wieso nimmt man jetzt den Tangens, wieso steht im tangens (-30). Ich bitte um Hilfe.

Comments

Ich kenne zwar die Lösung schon ... verstehe ich sie überhaupt nicht.

Dann schreibe sie hin :)  .... damit man sieht, was Du nicht verstehst.

Aber wieso nimmt man jetzt den Tangens

Wer nimmt wie wo den Tangens?

---

Lösung:

Die steilste Stelle des Deichs auf der Flussseite stimmt mit der Wendestelle xw des Profilgraphen überein. Da die Ableitung der Funktion für jede Stelle des Graphen den Tangens des Steigungswinkels angibt und die Steigungen auf der Flussseite alle negativ sind, lautet die Bedingung:

g(x)= tan(-30°) ⇒ k/1000 (3xw^2 -100*xw+625) ≈ -0,577

Setzt man für x w = 50/3 ein, so erhält man: k/1000*(3*(50/3)^2-100*50/3+625)≈-0,577

Durch Vereinfachung ergibt sich: k/1000*(2500/3 - 5000/3 + 1875/3) ≈ -0,577

k/1000*(-625/3)≈ -0,577

-5/24k≈ -0,577

Answer 1

Den Tangens nimmt man, weil der Tangens des Winkels gleich der Steigung ist, und das Minus nimmt man, wenn die Neigung abwärts geht (der Fluss rechts vom Deich gezeichnet ist).

Comments

Die erste Ableitung von g_k(x) an der Wendestelle x = 50/3 soll gleich minus tan(30°) sein:

\(\displaystyle -\frac{5}{24}\cdot k = \underbrace{- \tan(30^\circ)}_{\large-\frac{1}{\sqrt{3}}} \quad \Longrightarrow \quad k = \frac{8 \sqrt{3}}{5} \)

Answer 2

Die Steigung eines Funktionsgraphen in einem Punkt, stimmt mit der Steigung der Tangente in diesem Punkt überein. Diese lässt sich - wie du schon richtig gesagt hast - mit der Ableitung an dieser Stelle berechnen.

Was bedeutet das geometrisch:

Da die Tangente eine Gerade ist, lässt sich die Steigung auch mit Hilfe des Steigungsdreiecks angeben. Der Steigungswinkel ist nun so definiert, dass man den Winkel von der \(x\)-Achse gegen den Uhrzeigersinn zur Tangente bestimmt:

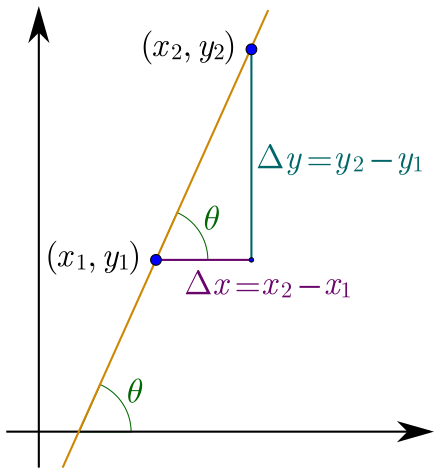
Quelle: https://de.wikipedia.org/wiki/Steigung

Wenn du dich noch an die Trigonometrie im rechtwinkligen Dreieck erinnerst, siehst man also, dass

\(m=\frac{\Delta y}{\Delta x}=\frac{\text{Gegenkathete}}{\text{Ankathete}}=\tan{\theta}\)

gilt.

Bei fallenden Geraden kann der Steigungswinkel daher auch größer als \(90°\) sein (mache dir das anhand einer Skizze klar). Allerdings ist es für die Praxis etwas sinnvoller, in so einem Fall negative Winkel anzugeben: Wir messen einfach den Winkel von der \(x\)-Achse im Uhrzeigersinn zur Gerade und da wir quasi falschrum messen, bekommt der Winkel entsprechend ein negatives Vorzeichen. Ein Steigungswinkel von \(150°\) entspricht also auch einem Steigungswinkel von \(150°-180°=-30°\). Die Umrechnung bekommt man also mit einer Verschiebung um \(180°\) hin.