Begründen oder widerlegen Sie...Ableitungen..??

Question

kann mir bitte jemand diese Aufgabe erklären: Begründen oder widerlegen Sie. a) Der Graph einer ganzrationalen Funktion zweiten Grades hat nie einen Wendepunkt. b) Jede ganzrationale Funktion dritten Grades hat genau einen Wendepunkt. c) Der Graph einer ganzrationalen Funktion n-ten Grades hat höchstens n Wendepunkte. d) Bei ganzrationalen Funktionen liegt zwischen zwei Wendepunkten immer ein Extrempunkt. -- vielen Dank schonmalim Voraus :-)

Answer 1

Hi,

Bedingung für einen Wendepunkt:

f''(x) = 0 und f'''(x) ≠ 0

 

a)

f(x) = ax²+bx+c

f'(x) = 2ax+b

f''(x) = 2a

--> brauchen wir gar nicht weitermachen. f''(x) immer ungleich 0, für a ≠ 0. (Und für a = 0 wärs keine Parabel mehr)

Falsch

 

b)

f(x) = ax³+bx²+cx+d

f'(x) = 3ax²+2bx+c

f''(x) = 6ax+2b

f'''(x) = 6a

--> Eine Gerade hat immer eine Nullstelle, also f''(x) = 0 erfüllt. Und f'''(x) ist eine Konstante und nie 0, also ebenfalls erfüllt.

Wahr

 

c)

Gleiches Spiel wie oben.

f(x) = xⁿ

f'(x) = n*x^n-1

f''(x) = n*(n-1)*x^n-2

--> Kann maximal n-2 Nullstellen haben und damit maximal so viele Wendepunkte.

Ob das jetzt wahr ist oder nicht, bleibt Dir überlassen, inwiefern Du "höchstens" verstehst. Als "kleinste obere Schranke" wäre die Aussage falsch ;).

 

d)

Gegenbeispiel:

f(x) = -x⁴+2x³

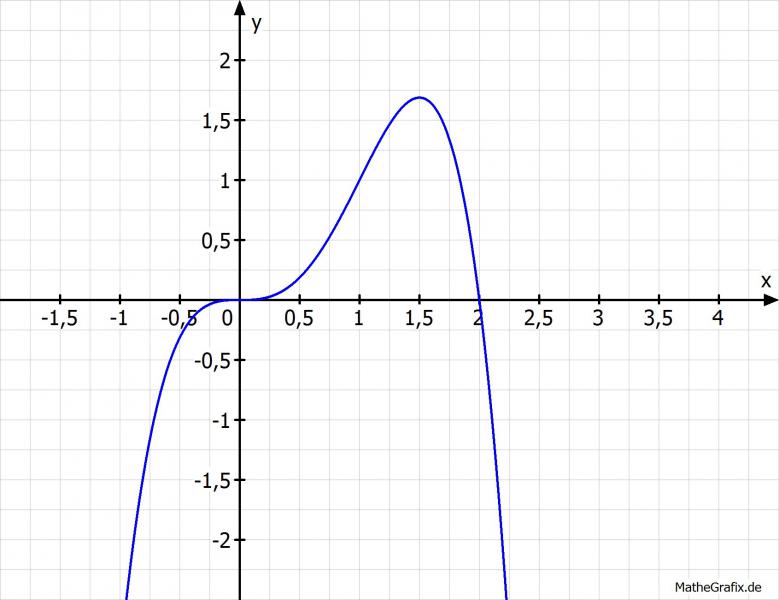
Falsch

 

Grüße

Comments

Die Antworten sind toll und echt leicht zu verstehen, nur hab ich eine kurze Frage.
So wie du die a) beantwortet hast müsste die Aussage doch wahr sein, oder?

---

Danke für das Lob :).

Nein, bei a) wird ja wegen des Wendepunkts f''(x) = 0 verlangt. Das aber ist nicht möglich, da für f''(x) = 2a für jedes beliebige x immer ein konstanter Wert rauskommt, welcher ungleich 0 ist (solange a ungleich 0, was wir voraussetzen) ;).

---

kannst du aufgabe b noch einmal erklären bitte

---

Und dabei auch Deine Antwort zur Aussage a) berichtigen...

---

@jd134: Danke^^. Habs geändert.

@hh220: Wenn Du mir sagst wo Du Probleme hast, helfe ich gerne ;).

Eigentlich leitest Du nur dreimal ab. Denn ein Wendepunkt ergibt sich, wenn f''(x) = 0 und f'''(x) ≠ 0 ist. Da wir abei f''(x) eine lineare Funktion haben, wenn wir es mit einer Funktion dritten Grades zu tun haben, dann haben wir auch eine Nullstelle. f''(x) = 0 können wir also erfüllen. Da nun f'''(x) = 6a ist, ist dies immer ein Wert ungleich 0 (solange a ≠ 0 ist, was wir voraussetzen, da wir sonst kein Polynom dritten Grades hätten). Damit haben wir gezeigt, wir haben immer nen Wendepunkt, und zwar genau einen, da eine lineare Funktion nur eine Nullstelle hat.

Alright? ;)

---

Zur aufgabe a:

Aber wenn die funktion f(x) zweiten grades ist, ist f''(x) doch nullten grades und somit eine parallele zur x-achse. Dann also hat sie keine nullstellen, wenn sie nicht genau auf der x-achse liegt

In der lösung ist a eine konstante, keine variable, also ist f''(x) auch eine parallele zur x-achse.