Berechne zunächst den Schnittpunkt von f und g und dann die Tangentensteigungen von f und g in diesem Punkt.
f ( x ) = g ( x )
<=> ( 2 x + 1 ) e - 1 / 2 x = e - 1 / 2 x
Beide Seiten durch e - 1 / 2 x dividieren:
<=> 2 x + 1 = 1
<=> 2 x = 0
<=> x = 0
Die x-Koordinate des Schnittpunktes ist also xs = 0
Die y-Koordinate ys findet man durch Einsetzen der x-Koordinate in eine der beiden Funktionsgleichungen (ich nehme g ( x ) ) :
ys = g ( 0 ) = e - 1 / 2 * 0 = 1
Somit hat der Schnittpunkt die Koordinaten
S ( xs | ys ) = ( 0 | 1 )
Die Tangentensteigungen mf von f bzw. mg von g in diesem Punkt sind die Funktionswerte der jeweiligen ersten Ableitungen, also:
f ' ( x ) = 2 * e - 1 / 2 x + ( 2 x + 1 ) * ( - 1 / 2 ) * e - 1 / 2 x
=> mf = f ' ( xs ) = f ' ( 0 ) = 2 + 1 * ( - 1 / 2 ) = 1,5
g ' ( x ) = ( - 1 / 2 ) * e - 1 / 2 x
=> mg = ( - 1 / 2 )
Für den Winkel alpha der Tangenten an f im Punkt S zur Horizontalen gilt nun:
tan ( alpha ) = mf
<=> alpha = arctan ( mf ) = arctan ( 1,5 ) ≈ 56,3 °
Für den Winkel beta der Tangenten an f im Punkt S zur Horizontalen gilt:
tan ( beta ) = mg
<=> beta = arctan ( mg ) = arctan ( -1 / 2 ) ≈ - 26,6 °
Somit ergibt sich der Schnittwinkel gamma der Grpahen von f und g zu:
gamma = alpha - beta = 56,3 ° - ( - 26,6 ° ) = 82,9 °
Dies ist der kleinere der beiden Schnittwinkel. Der größere Schnittwinkel delta ergibt sich, indem man rechnet:
delta = ( 360 - 2 * gamma ) / 2 = 180 - gamma = 97,1 °
Hier ein Schaubild der Graphen von f (blau) und g (rot).
Eingezeichnet sind weiterhin die Tangente an f (violett) im Punkt S ( 0 | 1 ) sowie die Tangente an g (grün) in diesem Punkte.
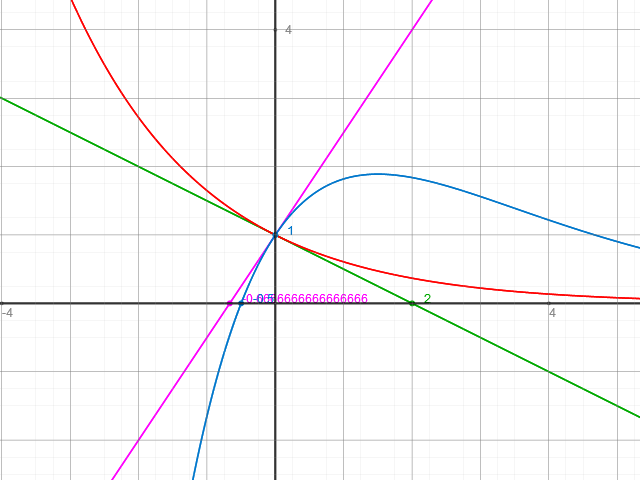
Man kann die Winkel zwischen den Tangenten am Bildschirm nachmessen und erhält (je nach Abbildungsgenauigkeit des Bildschirms) in etwa die berechneten Werte.