Gesucht ist die Summe der Quadratumfaenge aller Quadrate

Question

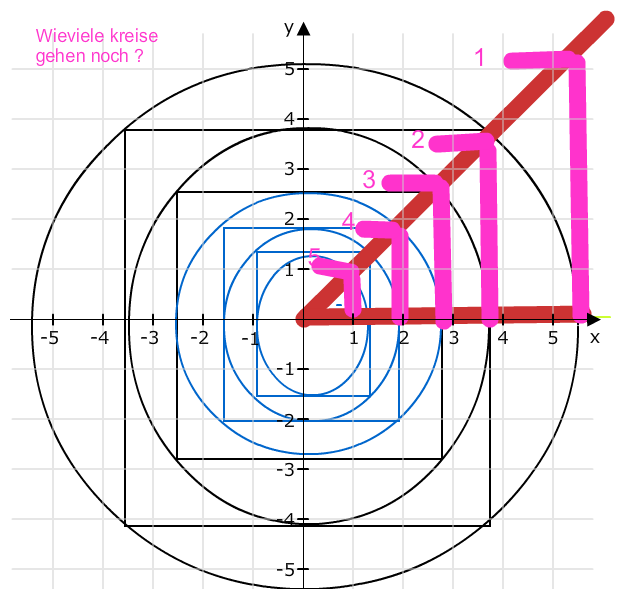
geg: Kreis D12cm darin ein Quadrat mit wiederrum einem kreis usw  ...Tangente hatt 45° 

Ges : Die anzahl der Kreise/und Quadrate  Max .

anschliessend deren Gesammtsumme ihrese Umfanges .

 

Zum einem Lösung per Steigungsdreieck (Pythagoras) zum anderen per Summenformel ...?

Ist als Grenzwert Radius 1.0? zu nehmen ?

Answer 1

Hi, die Radien der Kreise verkürzen sich jeweils mit dem Faktor \( \frac{1}{\sqrt{2}} \) damit bekommst Du eine geometrische Reihe die für den Umfang der Kreise gegen \( 2 \pi r ( 2+\sqrt{2} )\) konvergiert. Es gibt natürlich unendlich viele Kreise. Fuer die Qudrate gilt eine aehnliche Formel die gegen \( 8r(2+\sqrt{2}) \) konvergiert.

Comments

gude danke erstmal

ist den die Grenze hierbei nicht 0

also minimalwert 0,18 "an"
Kreisanzahl 6 ?

---

Der Grenzwert der Radien bzw. der Seitenlängen des Quadrats ist schon 0. Es gibt aber unendlich viele Kreise und Quadrate die immer kleiner werden. Die Summe der Umfänge der Kreise bzw. der Quadrate ist natürlich nicht 0, sondern wie angegeben. Ich bin übrigens davon ausgegangen das auch ein Quadrat mit Seitenlänge 12 existiert. Ansonsten muss man diese Umfang abziehen.

---

gude

also das erste quadrat hat die seiten länge 8,485cm
Durchmesser 12cm gilt nur für den ersten Kreis !

---

Ich habe noch um den ersten Kreis ein Quadrat gebaut.