ich bräuchte mal Hilfe bei folgender Aufgabe.
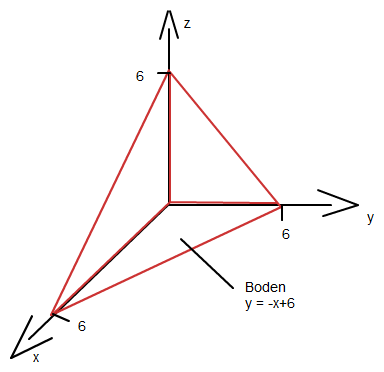
Die Ebene x+y+z = 6 bildet mit den 3 Koordinatenebenen eine gleichseitige Pyramide.
a) Bestimme das Volume
b) Bestimme die Schwerpunktkoordinaten
Bilden des dreifach Integrals sollte doch so aussehen.
Doch was möchte ich ableiten bzw. was ist mein f(x,y,z) welches in die Klammer kommt?
\( \int \limits_{x=0}^{6} \int \limits_{y=0}^{-x+6} \int \limits_{z=0}^{6-x-y}(\ldots) d z\, d y\, d x \)