Berechnung der Gleichung 2sin(x)+3cos(x)=4 mit der Hilfswinkelmethode?!

Question

Kann mir jemand sagen, wie ich die Gleichung löse und wie das mit der Hilfswinkelmethode funktioniert (hab den Begriff noch nie gehört)

Answer 1

2sin(x) + 3cos(x) = 4
sin(x) + 3/2*cos(x) = 2
sin(x) + tan(56,31)*cos(x) = 2
sin(x)*cos(56,31) + sin(56,31)*cos(x) = 2*cos(56,31)
sin(x + 56,31) = 1,109

Damit gibt das für x hier keine Lösung

Jetzt noch eine Skizze um das zu prüfen

Hier gibt es auch keine Lösungen wie man sieht.

Comments

Ich mache mal eine allgemeine Herleitung

Answer 2

Die Hilfswinkelmethode wird: S. 32/33 beschrieben.

http://www.abz.inf.ethz.ch/media/archive1/lehrmittel/hauptneu.pdf

Bitte nachrechnen und ggf korrigieren

2sin(x)+3cos(x)=4

Man wählt hier

2 = r cos Q ,  3 = r sin Q, c = 4

r cos Q sin x + r sin Q cos x = 4            |:r

sin (x + Q) = 4/r

x + Q = arcsin (4/r)

x =  arcsin (4/r)     -  Q

Jetzt erst mal Q und r bestimmen.

2 = r cos Q ,  2/r = cos Q

3 = r sin Q , 3/r = sin Q

tan Q = 3/2

Q = arctan (1.5)

r = 3 / sin Q = 3 / sin (arctan ( 1.5))

Jetzt einsetzen:

x  = arcsin (4/r) - Q

x =( arcsin ( 4 sin (arctan (1.5)) / 3)    - arctan (1.5)

x = 0.588003… - 0.463599 …i

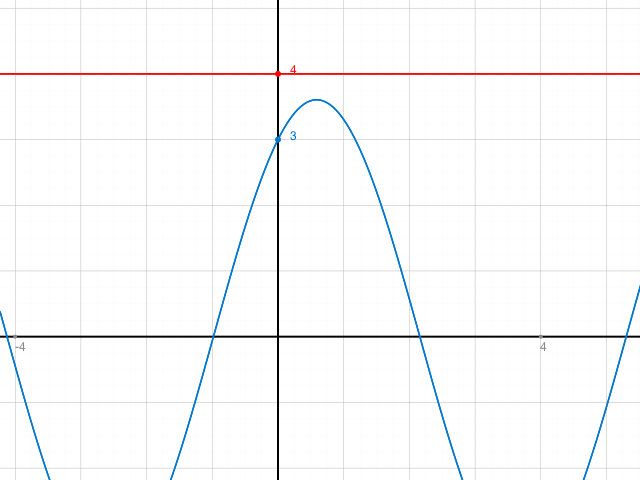
Es scheint hier nur komplexe Lösungen zu geben. Vgl. Graph von linker und rechter Seite der Gleichung.