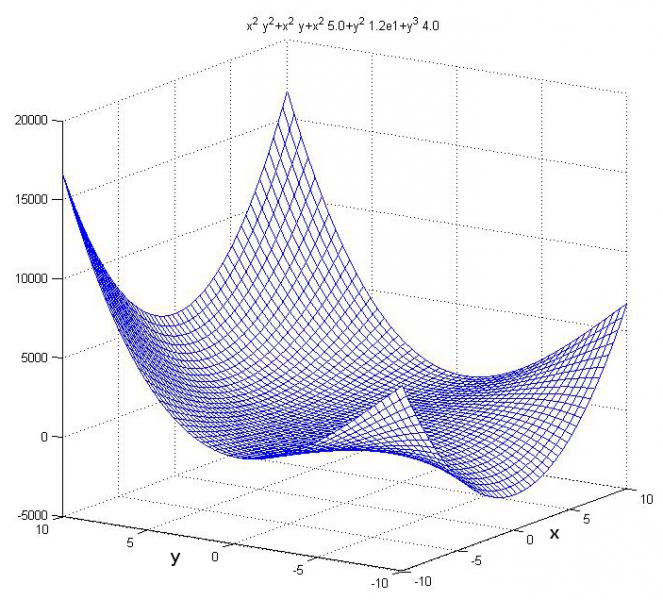
Berechnung der Extremwerte von f(x,y)= x² y² + x² y + 5x² + 4y³ + 12y²
Vorbemerkung:
Extremwerte von f(x,y) können nur in Punkten (x0, y0) auftreten, in denen
A die partiellen Ableitungen verschwinden
fx= fy= 0, (sog. stationärer Punkt)
B die partiellen Ableitungen nicht existieren
speziell: Randpunkte // wird hier nicht betrachtet
Rechnung:
Berechnung der Koordinaten der Extrempunkte:
fx= 2x * (y^2 + y + 5)
fy= 2x^2y + x^2 + 12y^2 + 24y
fx= 0:
* ist erfüllt für x = 0
* für x =/= 0, kann die Funktion nicht 0 werden, wenn y ∈ ℝ, y ist beliebig
fy= 0:
* da es nur bei x=0 für fx die Möglichkeit gibt 0 zu werden braucht bei fy für x nur 0 eingesetzt werden.
* fy(x=0, y): 12y^2 + 24 = 0, 12y * (y + 2) = 0. Man erhält also für fy= 0, y1= 0 und y2= -2.
Für die Extrempunkte gilt:
P1(0, 0), P2(0, -2)
Bestimmung der Art der Extrempunkte:

fxx= 2 * (y^2 + y + 5); fxx(P1) = 10; fxx(P2) = 20;
fxy= 2x * (2y + 1); fxy(P1) = fxy(P2) = 0;
fyy= 2x^2 + 24y + 24; fyy(P1) = 24; fyy(P2) = -24;
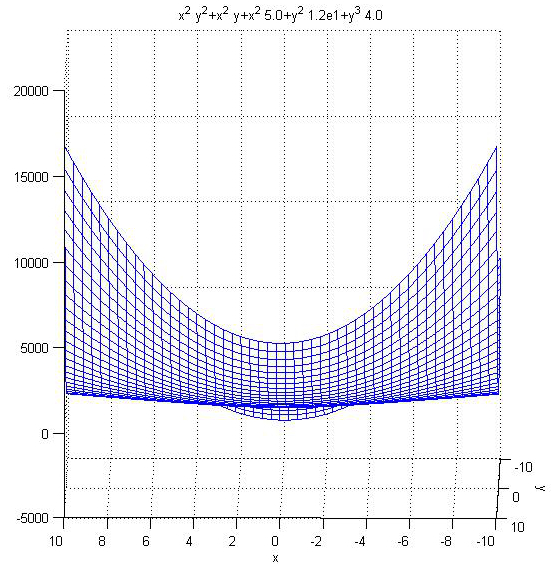
D(P1) = 240 > 0 und fyy(P1) = 24 > 0 ⇒ rel. Minimum bei P1(0, 0)
(Skizze: Aus dieser Perspektive kann man gut das Minimum erkennen)
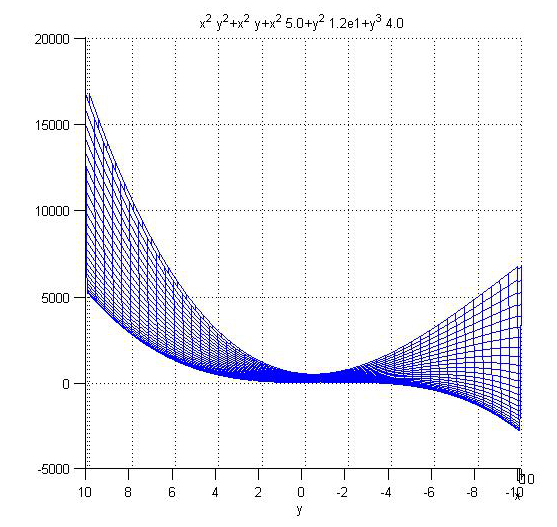
D(P2) = -480 < 0 ⇒ kein Extremwert, Sattelpunkt bei P2(0, -2)
(Skizze: Aus dieser Perspektive kann man gut den Sattelpunkt erkennen)
(Basierend auf: Merziger, G.; Formeln + Hilfen zur Höheren Mathematik; Binomi Verlag, Hannover 2007; S.132)