Rationale Zahlen und Rechenaufgaben

Question

ich brauche bei einer Aufgabe eure Hilfe.

Gegeben ist die Funktion f mit f_k(x)=x³-3x²+k, k>0

1) Ermittle die lokalen Extrempunkte und den Wendepunkt der Funktion f_k(x) (Für k habe ich 4 herausbekommen. Müsste auch richtig sein, also lautet die Funktion f_k(x)=x³-3x²+4). Berechne ihr Verhalten im Unendlichen. (Extrema und Wendepunkt habe ich schon herausgefunden, nur Verhalten im Unendlichen ist schwierig -> HP(0/4), TP(2/0), WP(4,6/40,3) (Korrigiert mich wenn ich Fehler gemacht habe :D). Skizziere anhand der ermittelten Ergebnisse anschließend den Graphen von f und die Wendetangente.

2) Wie verändert sich die Lage des Wendepunktes, wenn für k immer größere Werte gewählt werden? (Eine Rechnung und Begründung wäre nett :))

3) Die Tangente im Wendepunkt W(1/2) der Funktion f_k bildet mit den Koordinatenachsen ein Dreieck. Wie groß ist der Flächeninhalt (OK, die Aufgabe ist ein bisschen ungünstig, aber wenn ihr es nicht wisst, könnt ihr mir vielleicht erklären was ich zu tun habe?)

Vielen Dank (Drückt mir die Daumen für die Mathearbeit morgen :D)

Comments

Ich drücke dir die Daumen.

---

Kannst du mir auch bei den Aufgabe helfen?

---

Na ja, "für k habe ich 4 herausbekommen" ist sicher nicht im Sine der Aufgabenstellung gewesen. Die beiden Extrempunkte und der einzige Wendepunkt sollen doch in Abhängikeit von k bestimmt werden.

---

Nein, die erste Aufgabe heißt ja: Wie muss k gewählt werden, damit x₀=2 eine Nullstelle der Funktion ist. Berechne die anderen Nullstellen. (Die Aufgabe habe ich nicht aufgeschrieben, weil ich die Antwort schon habe).

Für k habe ich 4 herausbekommen und die Nullstellen lauten 2,2,-1 (2 und 2, weil eine doppelte Nullstelle vorliegt...)

Wäre aber nett wenn du mir trotzdem helfen könntest...

---

Ok, wir arbeiten also zunächst mit k=4. Deine Extrempunkte Stimmen, der Wendepunkt ist falsch, die Wendestelle muss schließlich zwischen den beiden Extremstellen liegen. Rechne also besser noch mal nach.

---

OK, zwar brauche ich bei den anderen Aufgaben Hilfe, wie z.B.: Verhalten im Unendlichen, aber ich will mal nicht so sein... Als Wendepunkt habe ich WP(1/2)...

Könntest du mir jetzt bitte bei den anderen Aufgabe helfen...

---

Das ist schon mal sehr gut, der Wendepunkt sollte sicher mit dem in Teil 3 angegebenen übereinstimmen :-)!

Zu den anderen Aufgabenteilen: "Verhalten im Unendlichen ist schwierig" Hm... das finde ich nicht. Alle f_k zeigen das gleiche Globalverhalten, sie verlaufen von −∞ bis +∞. Das liegt daran, dass es sich jeweils um ganzrationale Funktionen ungeraden Grades mit positivem Leitkoeffizienten handelt. Anders ausgedrückt: Das höchstgradige Monom bestimmt das Globalverhalten, hier also x³.

---

Kannst du mir das bitte nochmal erklären, irgendwie versteh ich das nicht so ganz, da wir erst letzte Woche damit angefangen haben

---

Kannst du mir auch bei den anderen Aufgaben helfen?

---

Mit der Frage nach dem "Verhalten im Unendlichen" -- man sagt manchmal auch "Globalverhalten" -- möchte man wissen, wie sich die Funktionswerte für sehr große oder sehr kleine Argumente (x-Werte) verhalten.

Bei ganzrationalen Funktionen gibt es nur vier verschiedene Fälle, die Du bitte in Deinem Schulbuch nachschlagen solltest. Welcher Fall eintritt, hängt immer vom höchstgradigen Monom, das ist der Summand im ausmultiplizierten Funktionsterm mit dem größten Exponenten (dem "Grad"), ab.

---

Ahhh, da gibt es ja die die 4 Globalverhalten... Erinnere mich wieder daran. Dankeschön

Wie siehts mit den anderen Aufgaben aus...Würdest du mir helfen oder hast du keine Lust... Ich schreib ja schon morgen leider... :(

---

"Skizziere anhand der ermittelten Ergebnisse anschließend den Graphen von f und die Wendetangente." meint, dass zunächst die Extrempunkte und der Wendepunkt in das Koordinatensystem eingetragen werden sollen und dann die Kurve verlaufsrichtig aber nicht unbedingt exakt durch diese Punkte gelegt werden soll.

---

Ohh man, die Aufgabe habe ich leider gerade in der halben Stunde gemacht. Hahaha, tut mir wirklich Leid.

Bei Aufgabe 2 und 3 noch bitte helfen, dann wärst du und ich endlich erlöst.

---

Zitat: "2) Wie verändert sich die Lage des Wendepunktes, wenn für k immer größere Werte gewählt werden? (Eine Rechnung und Begründung wäre nett :))"

Rechnungen werden hier wohl weniger erwartet. Wird k=4 durch k=6 ersetzt, verschiebt sich der Graph bei gleichem Kurvenverlauf  um zwei Einheiten nach oben. Das gilt dann natürlich auch für den Wendepunkt.

---

Wow, ich glaube mit mehr Mühe hätte ich das mit Leichtigkeit auch herausgefunden. Danke.Ich glaube ich habe mich eher auf die Rechnung und nicht auf die Begründung konzentriert, habe es aber irgendwie nicht verstanden.
Kannst du mir bitte noch bei Aufgabe 3 helfen...Mist, hättest du das Ganze als Antwort angegeben und nicht als Kommentar, hättest du dir auf jeden Fall ein Sternchen verdient...

---

Zitat: "3) Die Tangente im Wendepunkt W(1/2) der Funktion f_k"

Zunächst muss die Tangentengleichung g(x)=m*x+b bestimmt werden.
Sie muss den beiden Bedingungen m=f'(1) und b=g(1)-f'(1)*1 genügen.
Schau mal, ob Du das hinbekommst, für die Klausur morgen wird das
genügen. Allgemein kann man sich eine Formel für eine Tangenten-
gleichung zurechtlegen; entsprechende Aufgaben kommen oft genug vor.

---

Vieln Dank für deine großartige Hilfe

Answer 1

Gegeben ist die Funktion f mit fk(x) = x^3 - 3·x^2 + k ; k > 0

a) Wie muss k gewählt werden, damit x = 2 eine Nullstelle der Funktion ist.

fk(2) = 2^3 - 3·2^2 + k = 0

k = 4

Im folgenden untersuchen wir die Funktion f(x) = fk(x), wobei für k der eben errechnete Wert genommen wird. Sollten Sie keinen Wert heraus bekommen haben rechnen Sie mit k = 4 weiter.

b) Berechne die weiteren Nullstellen von f(x).

f(x) = x^3 - 3·x^2 + 4 = 0

(x^3 - 3·x^2 + 4) : (x - 2) = x^2 - x - 2

x^2 - x - 2 = 0

x = 2 ∨ x = -1

c) Ermittle die lokalen Extrempunkte und den Wendepunkt der Funktion f(x).

f(x) = x^3 - 3·x^2 + 4

f'(x) = 3·x^2 - 6·x

f''(x) = 6·x - 6

Extrempunkte f'(x) = 0

3·x^2 - 6·x = 3·x·(x - 2) = 0

x = 0 ∨ x = 2

f(0) = 4 → Hochpunkt (0 | 4)

f(2) = 0 → Tiefpunkt (2 | 0)

Wendepunkte f''(x) = 0

6·x - 6 = 0

x = 1

f(1) = 2 → Wendepunkt (1 | 2)

d) Berechne ihr Verhalten im Unendlichen.

lim (x → - ∞) f(x) = - ∞

lim (x → - ∞) f(x) = ∞

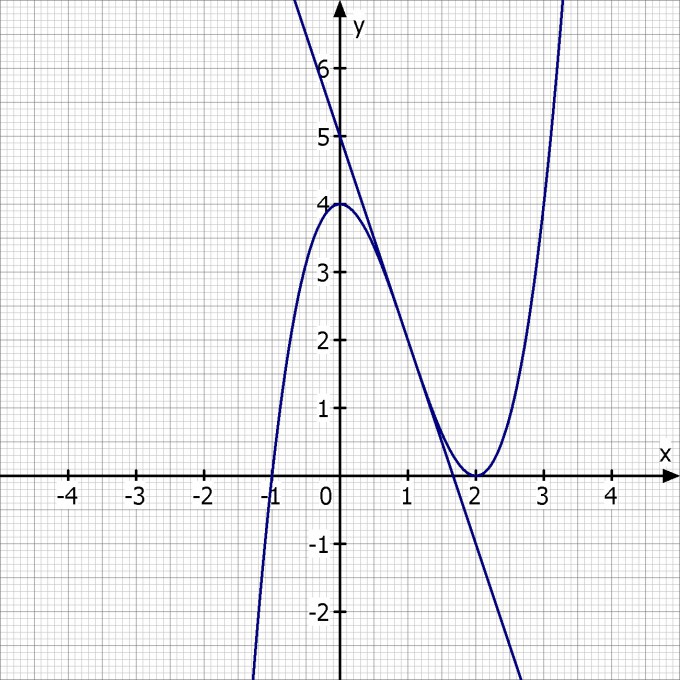
e) Skizziere anhand der ermittelten Ergebnisse anschließend den Graphen von f und die Wendetangente.

t(x) = f'(1)·(x - 1) + f(1) = 5 - 3·x

f) Wie verändert sich die Lage des Wendepunktes, wenn für k immer größere Werte gewählt werden?

Der Wendepunkt verschiebt sich nach oben.

g) Die Tangente im Wendepunkt W(1 | 2) der Funktion f bildet mit den Koordinatenachsen ein Dreieck. Wie groß ist der Flächeninhalt?

t(x) = 5 - 3·x

t(0) = 5

t(x) = 5 - 3·x = 0

x = 5/3

A = 1/2 · 5 · 5/3 = 25/6 = 4.167