Gegeben sei der Graph einer ganzrationalen Funktion dritten Grades.
f(x) = ax^3 + bx^2 + cx + d
f '(x) = 3ax^2 + 2bx + c
Dieser schneidet die x-Achse bei -1
f(-1) = 0
-a + b - c + d = 0
und -4
f(-4) = 0
- 64a + 16b - 4c + d = 0
und hat im Punkt (-2/-1)
f(-2) = -1
- 8a + 4b - 2c + d = -1
eine Steigerung von 1,5.
f '(-2) = 1.5
12a - 4b + c = 1.5
Du hast jetzt also ein lineares Gleichungssystem welches du mti dem Additionsverfahren lösen kannst
-a + b - c + d = 0
- 64a + 16b - 4c + d = 0
- 8a + 4b - 2c + d = -1
12a - 4b + c = 1.5
I - II und I - III
63a - 15b + 3c = 0
7a - 3b + c = 1
12a - 4b + c = 1.5
I - 3*II und I - 3*III
42a - 6b = -3
27a - 3b = - 9/2
I - 2*II
- 12a = 6
a = -0.5
42(-0.5) - 6b = -3
b = -3
7(-0.5) - 3(-3) + c = 1
c = -4.5
-(-0.5) + (-3) - (-4.5) + d = 0
d = -2
Also lautet der Funktionsterm
f(x) = ax^3 + bx^2 + cx + d
f(x) = -0.5x^3 - 3x^2 - 4.5x - 2
Ich mache mal eine Skizze
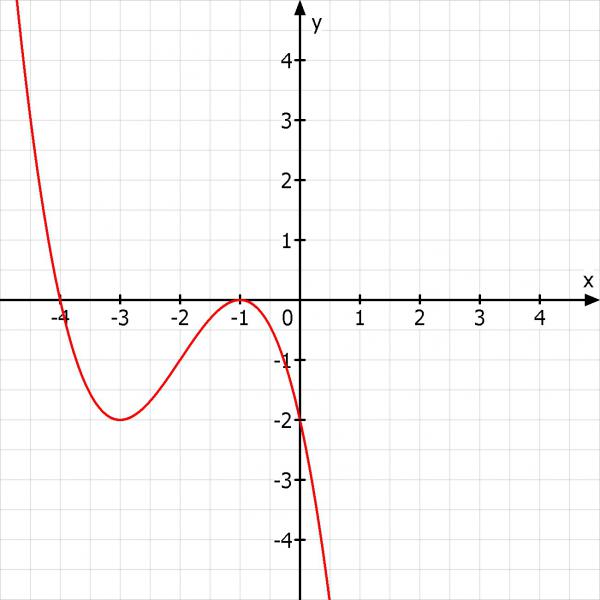
Wie wir sehen ist eine Bedingung nicht ganz erfüllt. Die x-Achse wird bei -1 nicht geschnitten sondern nur berührt. Es gibt also keine Funktion 3. Grades, die diese Bedingungen exakt erfüllt.