Funktionenschar - x3-ax2-x+a Nullstellen?

Question

f_a(x) = x³-ax²-x+a

also würde es a

x³-ax²-x+a = 0

heissen, um Nullstellen zu berechnen.

Wie berechnet man hiervon die Nullstellen? Muss man das irgendwie mit der Polynomdivision machen? Wie geht das?

Answer 1

ne Polynomdivision kannst Du machen. Hier ists aber wesentlich einfacher kurz die Augen aufzumachen. Es sticht geradezu heraus^^.

x³-ax²-x+a= 0

x²(x-a) - (x-a) = 0

(x-a) * (x²-1) = 0

Nullstellen kann man nun ablesen (letzteres ist die dritte binomische Formel)

x₁ = a

x_2,3 = ±1

Alles klar? :)

Grüße

Comments

Sehr schön, das gibt 'nen Daumen für Dich und ein Bookmark für mich :-)

---

Haha, danke Dir ;).

Ich hoffe Du bist nicht erblindet^^.

---

Nein, ich wurde erleuchtet aber nicht geblendet :-D

---

okay, und wenn man das Extrema berechnet, ist dann die erste Ableitung:

3x²-2ax-1 ?

---

Das ist korrekt :).

f'(x) = 3x²-2ax-1

Answer 2

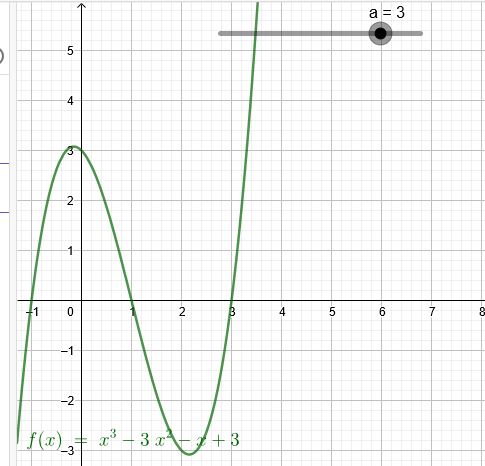
$f(x)=x^3-a*x^2-x+a$

Ich nehme mal $a=0$

$f(x)=x^3-x$

Nullstellen:

$x^3-x=0$

$x*(x^2-1)=0$

Satz vom Nullprodukt:

$x_1=0$   $f(0)=0^3-a*0^2-0+a=a$

$x_2=-1$   $f(-1)=(-1)^3-a*(-1)^2-(-1)+a=-1-a+1+a=0$

$x_3=1$     $f(1)=1^3-a*1^2-1+a=1-a-1+a=0$

Es liegen also immer bei $x=+-1$ die Nullstellen.

Die weiteren Nullstellen lassen sich nun mit der Polynomdivision finden:

   $(x^3-a*x^2-x+a):(x^2-1)=x-a$

$-(x^3-x)$

..............

         $-ax^2+a$

   $-(-ax^2+a )$

..............................

           0

Die 3. Nullstelle liegt bei $x=a$