Berechne die Länge der Riemen, wenn der Riemen gerade/gekreuzt geführt wird

Question

ich bin total verzweifelt! sitze jetzt schon seit drei stunden an diesem beispiel

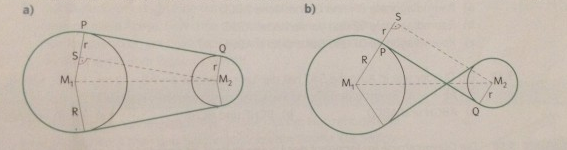
Zwei Riemenscheiben haben die Radien R = 80 cm und r = 40 cm. Ihre Mittelpunkte sind 225 cm voneinander entfernt. Berechne die Länge des Riemens, wenn der Riemen

a) gerade, b) gekreuzt geführt wird!

Hinweis: Ziehe eine Parallele zu PQ durch M₂ und betrachte das rechtwinkelige Dreieck M₁M₂S!

 

Kann mir bitte jemand bei a helfen? Ich bin  gerade voll verzweifelt

Answer 1

Was hast Du in den drei Stunden gemacht?

Die Strecke zwischen den Achsen ist gegeben und die andere Kathete ist die Differenz der Radien.

Der olle Grieche ist ja wohl bekannt und aus den Seitenverhältnissen lässt sich mit trigonometrischen Funktionen der Winkel bestimmen.

Aus dem Winkel die Umlauflänge des Riemens auf den Scheiben.

Comments

Wie meinst du das? Kannst du es vielleicht für mich aufschreiben? Das wäre voll nett!!

---

S -M1 -M2 bilden ein rechtwinkliges Dreieck. Welche Strecken sind gegeben?

---

HDen Abstand von den jeweiligen Mittelpunkten und die jeweiligen Radien! Das wäre wirklich voll nett, wenn du das Beispiel für mich machen könntest! Danke schon im Voraus

---

die Strecke MS ist wielang ?

---

Von M1 zu M2 sind es 225 cm

---

das steht in den Angaben - aber wo liegt S ?

---

S ist oberhalb von M1

---

und mit welchem Abstand ?

---

Keine Ahnung :)

---

R-r

das wäre die andere Kathtete. jetzt Hypothuse berechnen.

---

Könntest du mir die Schritte ganz genau erklären? ( Formel hinschreiben) bzw. Könntest du es mir vielleicht ausrechnen und das Ergebnis dann sagen und wie u zu dem gekommen bist? Du würdest mir wirklich das Leben retten! !

---

warum willst du nicht verstehen?

ist das so schwer zwei Zahlen voneinander abzuziehen ?

---

Nein! Aber ich verstehe nicht ganz wie ich dann zur gesuchten Antwort komme? Denn es ist ja gefragt die länge des Riemens

---

dann mach doch einfach Schitt für Schritt mit, wozu ich Dich anleite.

---

Ok! Bitte Schritt für Schritt sagen!

---

R-r

das wäre die andere Kathete. Jetzt Hypotenuse berechnen.