zuerst solltest du dir eine Funktionsgleichung für den Tunneldurchgang überlegen. Es gibt eine kreisförmige Funktion: y = √(r² - x²), wobei r der Radius ist. Wähle hierzu die Hälfte der kompletten Tunnelbreite (4,5 m).
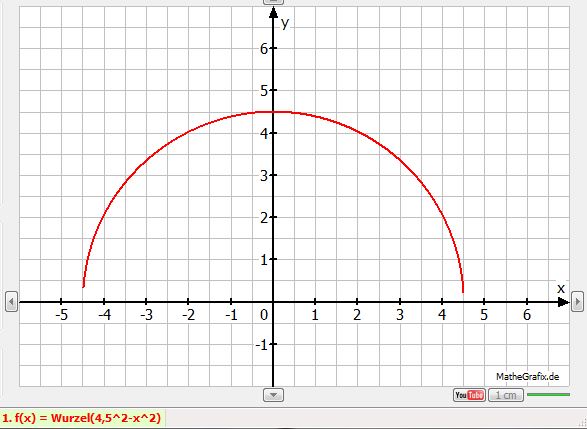
f(x) = y = √(4,5² - x²).
Nun kannst du einfach den kritischen Punkt in die Funktion einsetzen: x = -3 (+3 geht natürlich auch, Gf ist achsensymmetrisch). Der y-Wert den du erhältst entspricht der Höhe b!
f(-3) = √(4,5² - (-3)²) = ...
Ich bekomme ca. 3,35 m. Der Transporter ist allerdings 3,50 m hoch.
Wann hat der Tunnel die Höhe 3,5 m? Die Frage ist wichtig, denn vielleicht könnte der Truck einfach weiter links fahren (vom Fahrer aus gesehen).
3,5 = √(4,5² - x²) ι ²
12,25 = 4,5² - x²
12,25 = 20,25 - x² ι -20,25
- 8 = - x² ι *(-1)
8 = x² ι √
x ≈ 2,83 m
Der Truck muss demnach 20 cm weiter von der rechten äußeren Spur entfernt fahren, damit er nicht an der Decke entlang schrammt. Zur Gegenfahrbahn fehlen dann noch 30 cm. Ich würde es nicht riskieren, aber in Mathe ist alles erlaubt :).
LG
Alex