Hi!
Ein Polynom ist ein Term, der durch Variabeln(meist x) mit Potenzen ( natürlichen Exponenten) geprägt ist. Auf meinem Wissenstand sind es nur Summen, das heißt + und - kommen vor.
Es gibt Polynome verschiedenen Grades. Beispiel:
Polynom dritten Grades: 6x³+3x-4
Polynom fünften Grades: 10x5 +4x3 -2x -1
Du siehst ein Polynom wird nach der höchsten Potenz "benannt"
Zudem gibt es noch Binome und Trinome. Das bezeichnet die Anzahl der Summen
Ein Binom ( Bi= 1) wäre a+b oder x6+z2 x-3
Ein Trinom (Tri=3): a2 + b4 +6
Nun zur Polynomdivision. (
) -
Song zur Polynomdivision, mit dem ich das Ganze auch begriffen habe- Dies ist eine Art der Lösung eines Polynoms. Dazu muss man den Term durch die
Linearfaktoren teilen, vergleichbar mit der
schriftlichen Division. Eventuell nochmal nachschlagen
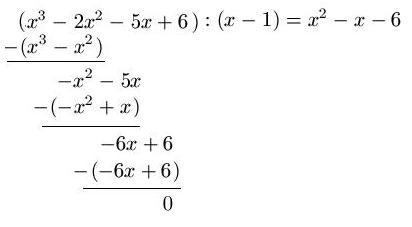
Erklären wir mal das Beispiel.
Du hast hier ein Polynom dritten Grades, erkennbar durch die Potenz 3.
Hier wurde das Polynom gleich Null gesetzt, sodass ein Wert x den ganzen Term= 0 bringt. Dieser x Wert war hier 1. Man muss diese Nullstelle raten, es handelt sich meist um + 1 ;- 1; +2 oder -2. Die Linearfaktorschreibweise lautet folgendermaßen: (x- Die geratene Nullstelle) also in diesem Falle ( x -(1) Wäre die Nullstelle -1 müsste es (x+1) heißen!
Nun zur schrittweisen Berechnung. x3 wird durch x geteilt. Das Ergebnis ist klar, x2 Dieses Ergebnis schreiben wir hinter das = Zeichen. Nun multiplizieren wir x2 mit dem Linearfaktor, also x2 * (x-1) = (x3 - x2)
Dies setzen wir nun, wie bei der schriftlichen Division unter ( x3 -2x2) und subtrahieren es. Heraus kommt -x2. Nun ziehst du -5x auf die Höhe des -x² und fährst erneut so fort.
1.) Nullstelle finden
2.) Linearfaktorschreibweise
3.Dividieren
--> Dabei immer das Ergebnis durch den Liearfaktor teilen, dieses wieder ausmultiplizieren und wieder subtrahieren. Nächsten Wert auf die Ebene "ziehen" und wiederholen. Durch das Video wird das hoffentlich klarer.
Gruß Luis