Folgendes Beispiel habe ich in zahlreichen Foren gefunden. Nur werde ich nirgends schlau. folgende Angabe haben alle Beitraege gemein: in ein Quadrat mit der Seitenlaenge a soll ein gleichschenkliges Dreieck mit maximalem Flaecheninhalt eingeschoben werden(Skizze). Ich habe versucht über die Umkehrung zu rechnen aber das funktioniert nicht weil ich keine Nebenbedingung finde. Koennt ihr mir bitte helfen?
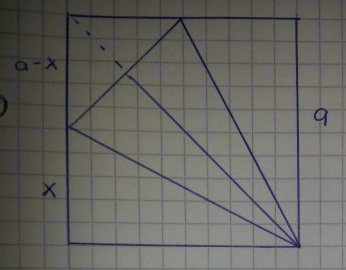
\( \begin{aligned} A \Rightarrow \min &=a x+\frac{1}{2} \cdot\left(a-x\right)^{2} \\ &=a x+\frac{1}{2} \cdot\left(a^{2}-2 a x+x^{2}\right) \\ &=\frac{1}{2}\left(a^{2}+x^{2})\right.\end{aligned} \)