Aufgabe:
Erhöhte Ozonkonzentrationen können beim Menschen Reizungen der Atemwege, Husten, Kopfschmerzen und Atembeschwerden bis hin zu Einschränkungen der Lungenfunktion und Lungenkrankheiten hervorrufen. Inr Ausmaß wird hauptsächlich durch die Aufenthaltsdauer in der ozonbelasteten Luft bestimmt. Befindlichkeitsstörungen wie Reizerscheinungen an Augen und Schleimhäuten werden vor allem durch Begleitstoffe des Ozons (im Sommersmog) hervorgerufen.
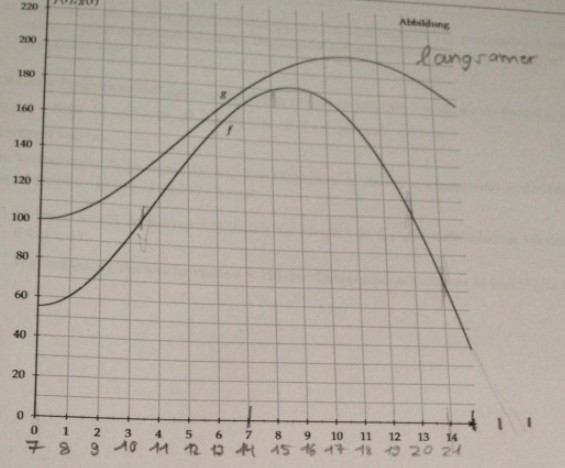
In einer Prognose für den kommenden Tag wird die Ozonkonzentration in einer Stadt zwischen 7 Uhr \( (t=0) \) und 21 Uhr \( (t=14) \) durch die Funktion \( f \) mit der Funktionsgleichung \( f(t)=0,06 \cdot\left(0,25 t^{4}-10,6 t^{3}+101,2 t^{2}\right)+55, \quad 0 \leq t \leq 14 \) (*)
und in einer ländlichen Region für denselben Zeitraum durch die Funktion \( g \) modelliert. ( \( t \) in Stunden; \( f(t), g(t) \) in \( \mu \mathrm{g} / \mathrm{m}^{3} \) )
Die Graphen von \( f \) und \( g \) sind in der Abbildung auf der nächsten Seite dargestellt.
(t-Achse: 1 LE entspricht 1 Stunde; \( f(t)-, g(t) \)-Achse: 1 LE entspricht \( 1 \mu \mathrm{g} / \mathrm{m}^{3} \) )
Aufgabe a)
(1) Vergleichen Sie die Graphen von \( f \) und \( g \) im gegebenen Sachzusammenhang.
(2) Geben Sie die Ozonkonzentrationen in der Stadt zu den Zeitpunkten 7 Uhr und 21 Uhr nach dem Prognosemodell an.
(3) Bestimmen Sie den Zeitpunkt, an dem die höchste Ozonkonzentration in der Stadt prognostiziert wird, und berechnen Sie die höchste Ozonkonzentration.
(*) Die Funktion \( f \) ist für alle \( t \in \mathbb{R} \) definiert, werden aber nur für \( 0 \leq t \leq 14 \) zur Modellierung verwendet.
Bei einer Ozonkonzentration von mindestens \( 180 \mu \mathrm{g} / \mathrm{m}^{3} \) muss die Bevölkerung über die Medien über die Ozonbelastung informiert werden.
Aufgabe b)
(1) Am kommenden Tag wird in der Stadt eine Ozonkonzentration von mindestens \( 180 \mu \mathrm{g} / \mathrm{m}^{3} \) während eines Zeitraumes von mehr als einer Stunde prognostiziert.
Begründen Sie dies unter Verwendung geeigneter Funktionswerte.
(2) Ermitteln Sie die Zeitpunkte, an denen die Ozonkonzentration in der Stadt am stärksten zuund am stärksten abnimmt.
(3) Bestimmen Sie die durchschnittliche Ozonkonzentration zwischen 7 und 21 Uhr.
(4) Begründen Sie, dass die Fortsetzung der Funktion \( f \) auf das Intervall \( [0 ; 24] \) zur Prognose der Ozonkonzentration nicht geeignet ist.
Ein Prognosemodell aus der Schweiz zur Berechnung der maximalen Ozonkonzentration des folgenden Tages lautet: \( \quad O_{m}=0,25 \cdot O_{h}+5,5 \cdot T_{m}-40 \).
\( O_{m}: \quad \) Maßzahl der maximalen Ozonkonzentration (in \( \mu \mathrm{g} / \mathrm{m}^{3} \) ), die für den morgigen Tag prognos tiziert wird
\( O_{h}: \quad \) Maßzahl der maximalen Ozonkonzentration \( \left(\mathrm{in} \mu \mathrm{g} / \mathrm{m}^{3}\right) \) am heutigen Tag
\( T_{m}: \quad \) Maßzahl der maximalen Temperatur \( \left(\right. \) in \( \left.{ }^{\circ} \mathrm{C}\right) \), die für den morgigen Tag prognostiziert wird Heute betrug die maximale Ozonkonzentration \( 120 \mu \mathrm{g} / \mathrm{m}^{3} \).
Ansatz/Problem:
Ich verstehe die 3. Aufgabe von b) nicht. Ich dachte das wäre die mittlere Änderungsrate. Ist es aber nicht.