Integral berechnen: x * e^-x: aber wie aufstellen UND wie "aufleiten" bzw. integrieren?

Question

ich kämpf mich grad durch Integrale und habe dazu das hier gefunden:

https://www.youtube.com/watch?v=2l2r2x502MI

aber so ganz komm ich damit nicht zurecht:

Mein Ansatz sieht bisher wie folgt aus:

Dazu hätte ich folgende Fragen:

1) Müssen meine Grenzen nicht berücksichtigt werden? Weil im Beispiellösung aus unserem Tutorium werden diese auch einfach weggelassen?


2) wie leite ich e^-x richtig auf (ich weiss den Begriff gibt es so eig. gar nicht) also wie komm' ich zur Stammfunktion mein ich. Hätte ich jetzt 6x, wüsste ich es glaub ich dann wäre doch die Stammfunktion: 

3x² oder?

3) Nachdem ihr mir vielleicht erklärt habt, wie ich zur Stammfunktion von e^-x komme, wie genau gehts dann weiter?
Bzw. was ist mein Ziel, ich hab hier zwar die Lösung aus unserem Tut, aber ich wills ja auch verstehen um zukünftig auch selbst anwenden zu können!


Musterlösung:




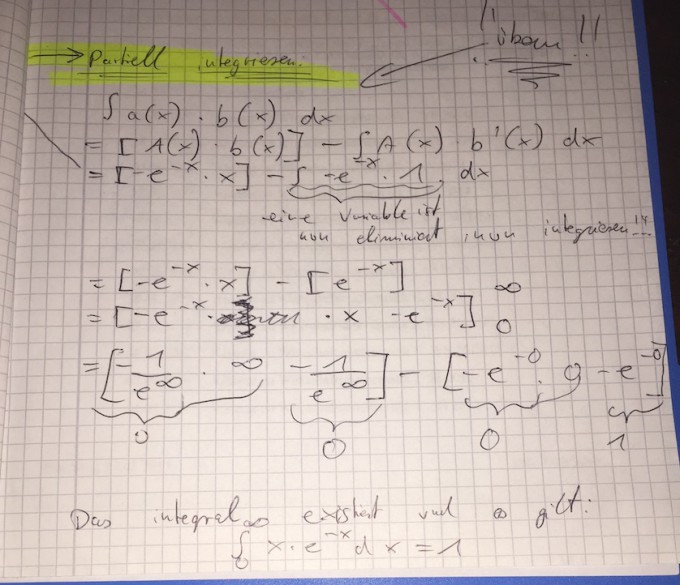
Danke vorab für Tips und Anregungen!

Edit: "ok hab jetzt gemerkt, dass wahrscheinlich e^-x integriert -e-x ist, soll ich mir das einfach merken oder hätte ich das auch irgendwie herleiten können damit ichs mir merken kann? ;)

die anderen Fragen wären dennoch meinerseits offen ;) THX

Answer 1

Deine Fragen und deine Lösungsversuche lassen darauf schließen das
du das Integrieren noch lernen willst.

1. beim Integrieren bilde ich zunächst die Stammfunktion.
Die Integrationsgrenzen lasse ich zunächst weg.
Die kommen zum Schluß.

2. Diese Aufgabe kann über das partielle Integrieren gelöst werden.
Das ergibt die Frage, welcher der beiden Faktoren soll auf- bzw. abgeleitet
werden. Hier hilft manchmal nur Probieren und beide Varianten durchzurechnen.

In diesem Beispiel stört das x. Dies könnte durch ableiten ( x ) ´ = 1 entfernt
werden. Also muß e^{-x}  aufgeleitet werden.

Dies mache ich meist durch Probieren. Eine e-Funktion kann nur aus einer e-Funktion
abgeleitet worden sein. Ich nehme die e-funktion und leite diese einmal ab.
[ e^{-x}  ] ´= e^{x} * ( -1)
Jetzt stört noch das (-1). Dies wird kompensiert durch die Gegenfunktion
[ - e^{-x}  ] ´ = (-1) * [ e^{-x} ] ´ = (-1 ) *  e^{-x} * ( -1 ) = e^{-x}
Da haben wir es schon. Also
∫ e^{-x}  dx = - e^{-x}

Die partielles Integration sieht dann folgendermaßen aus.

Comments

na das wahr mal eine Antwort ich danke Dir sehr dafür!

Ich werde das jetzt mal in aller Ruhe durchgehen und verinnerlichen ;)

Grüße

Alex

---

kurze Frage noch und zwar hab ichs jetzt so gemacht:

ich weiß ich bin noch nicht fertig, nur ich bin etwas durcheinander ich hab in unserem Tutorium das hier als Lösung:

also entweder ist die Lösung von dir etwas anders oder sie ist genau das Gleiche, aber ich verstehe es nur nicht ganz :D 

Oder Du hast jetzt nur integriert ohne diesen letzten Schritt mit Lambda noch durchzuführen, weil diesen Schritt mit den Grenzen in diesem Fall gegen unendlich und mit Lambda usw. muss ich doch bei jeder partiellen Integration am Ender auch noch machen oder?



Gruß

---

Die richtige Stammfunktion ist auf jeden Fall
e^-x·(-x - 1)
oder
( -e^-x ) ·( x + 1)

Du willst noch berechnen

[ e^-x·(-x - 1) ] ₀ ^∞
e^-∞·(-∞ - 1)  - ( e^-0·(-0 - 1) )
Ohne Nachweis
e^-∞·(-∞ - 1) = 0 ( -∞ - 1 ) = 0

0 - ( e^-0·(-0 - 1) )
0 - ( 1 * -1 ) = 1

---

ok danke, das hilft nochmal weiter....

ich muss jetzt erst mal üben üben üben... mit dem neuen Wissen :D

---

Durch das Lösen von Aufgaben und das Bewältigen von auftretenden
lernt man wohl am meisten.
Aber auch : nicht mit dem Kopf durch die Wand wollen.
Wird es doch zu verwirrend dann lieber mal das Heft zuklappen
und Fußball spielen gehen.

Answer 2

∫ x·e^{-x} dx = x·(-e^{-x}) - ∫ 1·(-e^{-x}) dx = - x·e^{-x} + ∫ e^{-x} dx = - x·e^{-x} - e^{-x} = e^{-x}·(-x - 1)

Die Integrationsgrenzen sind erstmal egal. Die sind eventuell nur wichtig bei einer Integration durch substitution wenn du nicht resubstituieren möchtest.

Comments

Hey Der_Mathecoach,

danke für die blitzschnelle Antwort ;)

Wie gesagt die Lösung hab ich ja schon ausm Tut von uns, aber könntest du vielleicht ein zwei Sätze dazu schreiben, was ich mir merken muss bzw, was ich immer machen muss um so ein Integral zu berechnen?

---

Ich bestimme zunächst IMMER das unbestimmte Integral. D.h. ich lasse IMMER die Integrationsgrenzen weg.

∫ f(x) dx = F(x) + C

Dann bestimme ich das bestimmte Integral mit der gefundenen Stammfunktion

∫ (a bis b) f(x) dx = F(b) - F(a)

---

Ich bestimme zunächst IMMER das unbestimmte Integral. D.h. ich lasse IMMER die Integrationsgrenzen weg.

Das glaube ich nicht. Wäre ja auch ziemlich dumm!

---

Es gibt Leute, die lesen IMMER nur den ersten Satz und lassen die weiteren einfach weg.

Unglaublich, aber ziemlich dumm!

---

Kannst du mirs dann nochmal erklären vlt?

---

Nach obiger rechnung kenne ich die Stammfunktion

∫ x·e^-x dx = e^-x·(-x - 1) 

Jetzt kann ich das bestimmte Integral berechnen

∫ (0 bis ∞) x·e^-x dx = (e^-∞·(-∞ - 1)) - (e^-0·(-0 - 1)) = 0 - (-1) = 1

---

Wenn du noch probleme mit dem integrieren der e-Funktion hast was sind die ersten drei Ableitungen von:

f(x) = e^{ax + b}

Fällt dir etwas auf? Wenn du mal schaust was bei der Ableitung passiert, was könnte man dann für das integrieren vermuten?

Bilde also auch mal die Stammfunktion von

f(x) = e^{ax + b}

Ob deine Stammfunktion richtig ist, kannst du sehen wenn du diese Ableitest. Dann sollte ja wieder f(x) heraus kommen.