Rekonstruktion: Polynom ist symmetrisch zum Ursprung und hat den Tiefpunkt (1/-2)

Question

Ich komme hier mit einer Aufgabe nicht weiter und hoffe, dass mir jemand helfen kann.

Die Aufgabe lautet: Eine Ganzrationale Funktion dritten Grades ist symmetrisch zum Ursprung des Koordinatensystems und hat den Tiefpunkt (1/-2). Wie lautet die Gleichung.

Ich komme auf die Bedingungen f(1)=-2   f `(1)=0 und f(0)=0

Ich frage mich jetzt, ob das korrekt ist, und wie ich auf die letzte Bedinung komme, welche ich zum Rechnen benötige.

Answer 1

Die Aufgabe lautet: Eine Ganzrationale Funktion dritten Grades ist symmetrisch zum Ursprung des Koordinatensystems

f(x) = ax³ + bx
f'(x) = 3ax² + b

und hat den Tiefpunkt (1/-2). Wie lautet die Gleichung.

f'(1) = 0
3·a + b = 0

f(1) = -2
a + b = -2

Deine Bedingungen sind richtig. f(0)=0 ist allerdings überflüssig, wenn die die Funktionsgleichung so aufstellst wie ich es oben gemacht habe.

Das LGS hat die Lösung: a = 1 ∧ b = -3

Die Funktion lautet daher:

f(x) = x³ - 3x

Skizze:

Comments

"Deine Bedingungen sind richtig. f(0)=0 ist allerdings überflüssig, wenn die die Funktionsgleichung so aufstellst wie ich es oben gemacht habe."

"f(x) = ax³ + bx
f'(x) = 3ax² + b"

Könntest du mir bitte erklären wie du auf die Funktion ax³+bx kommst?

Da f(0)= 0 ist würde die Funktion ja ax³+bx²+cx lauten da wir wissen das d=0 ist. Ich verstehe nicht wie du sofort das ^2 von b und cx weg bekommst.

Ich komme nur auf 3 Ansätze:

f   (0)=0

f ' (1)=0

f  (1)=0

---

Eine ganzrationale Funktion dritten Grades ist symmetrisch zum Ursprung des Koordinatensystems.

Das symmetrisch zum Ursprung verrät uns das wir nur ungerade Potenzen von x haben. Also fällt x² und x⁰ hier weg.

f(x) = ax³ + bx² + cx¹ + dx⁰

Es bleibt also

f(x) = ax³ + bx

---

Ich verstehe ja nicht wieso die ungeraden Potenzen wegfallen wenn es zum Urpsrung symmetrisch ist. Als Merksatz könnte ich es mir ja merken dennoch hab ichs nicht verstanden.

Was bewirken denn die geraden Potenzen?

---

Gerade Potenzen sind symmetrisch zur y-Achse. Denke an a oder ax^2 oder an ax^4 ...

---

und ungerade Potenzen symmetrisch zur x Achse?

---

Nein. Ungerade sind Punktsymmetrisch zum Ursprung. Denke an ax oder an ax^3 ...

Answer 2

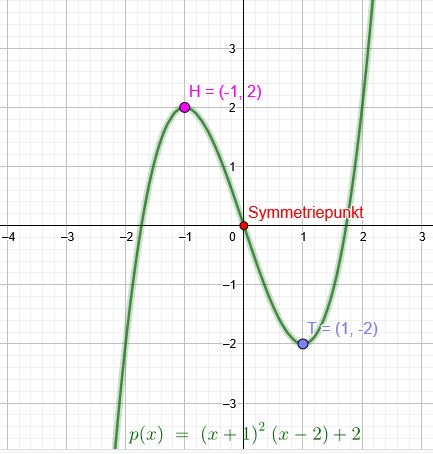
Eine ganzrationale Funktion dritten Grades ist symmetrisch zum Ursprung des Koordinatensystems und hat den Tiefpunkt $T(1|-2)$. Wie lautet die Gleichung?

Punktsymmetrie zum Ursprung bedeutet hier: Hochpunkt $H(-1|\red{2})$

Ich verschiebe nun den Graph um $\red{2}$  nach unten. $H´(-1|0)$ Hier ist nun eine Zweifachnullstelle.

$f(x)=a ( x+1)^2(x-N)$

Ursprung: $O(0|0)$ → $O´(0|-2)$

$f(0)=a ( 0+1)^2(0-N)=-a N$

$-a N=-2$  → $a =\frac{2}{N}$

$f(x)=\frac{2}{N} ( x+1)^2(x-N)$

$T(1|-2)$→ $T´(1|-4)$

$f(1)=\frac{2}{N} ( 1+1)^2(1-N)=\frac{8}{N} (1-N)$

$\frac{8}{N} (1-N)=-4$    → $\frac{8}{N} (N-1)=4$  → $\frac{2}{N} (N-1)=1$ → $N=2$      $a =1$

$f(x)=( x+1)^2(x-2)$

Jetzt um $\red{2}$  nach oben:

$p(x)=( x+1)^2(x-2)+2$