1. Kannst du mit dem Funktionsplotter dieser Seite selbst zeichnen.
2. Wie lautet die Gleichung einer nach unten geöffneten Standardparabel mit Scheitel (5|2)?
y = (x-5)^2 + 2 = x^2 - 10x + 25 + 2 = x^2 - 10x + 27
3. Wodurch unterscheiden sich die Parabel y = 3x² - 18x + 27 und y = 1/3x² - 2x + 3?
Man erhält die zweite durch Division durch 9. Das ist eine Stauchung in y-Richtung mit dem Faktor 1/9. Die Öffnung ist unterschiedlich. Die Nullstellen sind gleich. Ebenso die Scheitelstelle. vgl. auch Kommentar unten.
4. Bestimmte den Scheitel der Parabel, die durch die Punkte A(-1|-38), B(1|-18) und C(3|-6) geht.
Ansatz
y = ax^2 + bx +c. Punktkoordinaten einsetzen
1. -38 = a - b + c |–
2. -18 = a +b +c
-----------------------------
20 = 2b → b=10
2.' -18 = a+10 + c |–
3. -6 = 9a + 30 + c
-----------------------------------
12 = 8a + 20
-8=8a → a=-1
In 3. -6 = -9 + 30 + c
-27 = c
y = -x^2 + 10x -27
Umwandlung in Scheitelpunktform mit quadratischer Ergänzung.
y= - (x^2 -10x + 25 - 25) - 27
y=-(x^2 - 10x + 25) + 25 - 27
y=-(x-5)^2 - 2
Scheitelpunkt ablesen: S(5|-2)
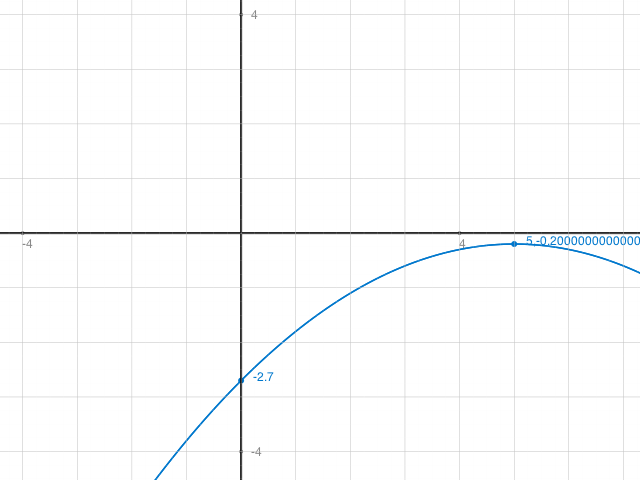
Hier zur Kontrolle der Graph: (Beachte y-Richtung um Faktor 10 gestaucht: 4 entspricht 40...)
Scheitelpunkt richtig bei (5, -2)
Ich habe das Folgende jetzt oben vorgerechnet. Hoffentlich kannst du's auf den Rest deiner Aufgaben übertragen. Betrachte erst mal noch die Videos.
Dann habe ich noch Probleme bei bestimmen einer Funktionsgleichung von der Parabel, z.B
Bestimmen Sie die Funktionsgleichung der Parabel in Scheitelform.
A: Y = ________
B: Y = ________
wo A und B die Parabel sind, und beim Einzeichnen einer Parabel wenn eine funktionsgleichung angegeben ist wie z.B y = x² + 2, y = (x + 2)², y = (x - 1)² - 3 und y = (x + 3)² + 1