Aufgabe zu Gasgeschwindigkeiten

Question

Hallo wir haben folgende Aufgabe:

"Sie haben über die Maxwell-Boltzmann-Verteilung gehört, welche die Teilchengeschwindigkeit im Gas beschreibt. Die Abbildung unten zeigt eine hypothetische Geschwindigkeitverteilunng für eine Probe von N Gasteilchen. Beachten Sie, dass P(v) = 0 für v > 2v₀                  

  (velocity = Geschwindigkeit)

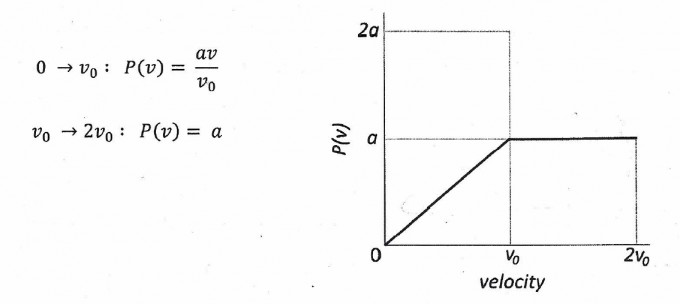
a) Geben sie a als eine Funktion von v₀ wieder: (für N Teilchen, ∫ P(v) dv = 1)

b) Wie viele von den N Teilchen haben eine  Geschwindigkeit zwischen 1.5 v₀ und 2 v₀?

c) Geben Sie einen Ausdruck für die Durchschnittsgeschwindigkeit v_quer indem sie v₀ brauchen.

d) Berechnen Sie die "root mean square" Geschwindigkeit (v^2)_quer

a) Hier habe ich einen Wert von 2/(3*v₀) erhalten, stimmt das?

b) Hier bin ich auf 33% gekommen, stimmt das?

c) Hier habe ich für v_quer (3*a*v₀)/4 erhalten, stimmt das?

d) Bei dieser Aufgabe komme ich nicht weiter, wie muss ich das berechnen?

Für Antworten binn ich dankbar :)

Answer 1

a) und b) passt.

c) passt nicht. Bist du sicher, dass du den Erwartungswert von \(v\) korrekt berechnet hast?

d) Berechne den Erwartungswert von \(v^2\). Für mich wäre aber die RMS-Geschwindigkeit die Wurzel aus \( \overline{v^2} \).

Gruß

Comments

Danke für die rasche Antwort!

bei c) habe ich (a/2)*(v₀/2)+(a/2)*v₀ gerechnet und dann aufgelöst, da ich aus dem zuerst linearen und dann konstantem Graph je die Hälfte genommen und dann addiert habe. Was wäre dann die richtige Vorgehensweise?

zu d) Die Aufgabe ist offiziell auf englisch verfasst und ich habe sie übersetzt. Original heisst es:

Calculate the root mean square velocity v² ← mit Querstrich oben drauf, wie du ihn in der Antwort gemacht hast

Wie kann ich dies berechnen?

---

So berechnet sich aber nicht die durchschnittliche Geschwindigkeit, das siehst du ja insbesondere daran, dass der Term den du raus hast gar keine Geschwindigkeit ist.

Richtig wäre es in diesem Fall den Erwartungswert zu berechnen, deine Geschwindigkeit ist ja die Zufallsvariable zu der du die Wahrscheinlichkeitsdichte vorliegen hast.

Somit wäre:

$$ \overline{v} = \mathbb{E}(v) = \int \limits_0^{2v_0} p(v) \cdot v dv = \int \limits_0^{v_0} \frac{2v^2}{3v_0^2} dv+ \int \limits_{v_0}^{2v_0} \frac{2v}{3v_0}dv$$

bei d) ist \(\overline{v^2} \) ja der Erwartungswert der quadrierten Geschwindigkeit, diesen berechnest du analog zu c) mittels:

$$ \overline{v^2} = \int \limits_0^{2v_0} p(v) \cdot v^2 dv $$

Wie gesagt kenne ich "root mean square speed" aber als \( v_{rms} = \sqrt{\overline{v^2}} \).

---

Oke super

Dann werde ich das in den nächsten Tagen mal druchrechnen probieren :)

---

Ich habe mir die Rechnung nochmals angeschaut und verstehe nicht ganz, warum du bei c) im Integral noch *v rechnest und ausserdem wie du auf die Brüche kommst, die integriert werden. Könntest du das eventuell genauer erklären?

---

Bin unterwegs deswegen nur die kurze Antwort. Bezüglich der Vorgehensweise kann ich dir nur raten mal was zu dem Thema Erwartungswert anzuschauen. Der Begriff ist nun schon mehrfach gefallen. Die Brüche entstehen dadurch dass ich das Ergebnis für a verwendet habe

---

Aha, ich habe völlig vergessen, dass p(v) im ersten Teil (a*v)/v₀ ist. Jetzt versteh ich es.

Kann es sein, dass die Lösung von c) (11*v₀)/9 als Durchschnittsgeschwindigkeit ist?

Und bei d) habe ich (3v₀² -16 v₀)/(18) für das Quadrat, bzw. v₁= 0 und v₂ = 16/3 für die Wurzel errechnet. Stimmt das?

---

sorry, d) habe ich falsch aufgeschrieben:

(31*v₀²)/18 für v2 quer und 1/3 * √(31/2) * v₀ nach dem ziehen der wurzel habe ich erhalten, stimmt das?

---

Ja das passt jetzt für c) und d) =).

---

Super, vielen Dank für deine Hilfe! :)