Bestimmung einer Funktion: f(x) = (a·x^3 + b)/(x^2 + c)

Question

Gegeben ist die Funktion f(x) = (a·x³ + b)/(x² + c).

Bestimmen Sie die Koeffizienten a,b,c ∈ Iℝ so dass, G_ƒ bei x = 3 ein relatives Extremum und bei x = 1 einen Pol erster Ordnung hat. Außerdem soll die Gerade mit der Gleichung y - 3x = 0 Asymptote.

Answer 1

f(x) = (a·x^3 + b)/(x^2 + c) = a·x + (b - a·c·x)/(x^2 + c)

Damit x = 1 eine Polstelle ist muss c = -1 sein.

y - 3x = 0
y = 3x 

ist Asymptote wenn a = 3

f'(x) = x·(a·x^3 + 3·a·c·x - 2·b)/(x^2 + c)^2
f'(x) = x·(3·x^3 - 9·x - 2·b)/(x^2 - 1)^2

 

Damit x = 3 ein Extremum ist muss die Ableitung dort Null sein

x·(3·x^3 - 9·x - 2·b) = 0
3·(3·3^3 - 9·3 - 2·b) = 0
b = 27

Damit lautet die Funktion

f(x) = (3·x^3 + 27)/(x^2 - 1)

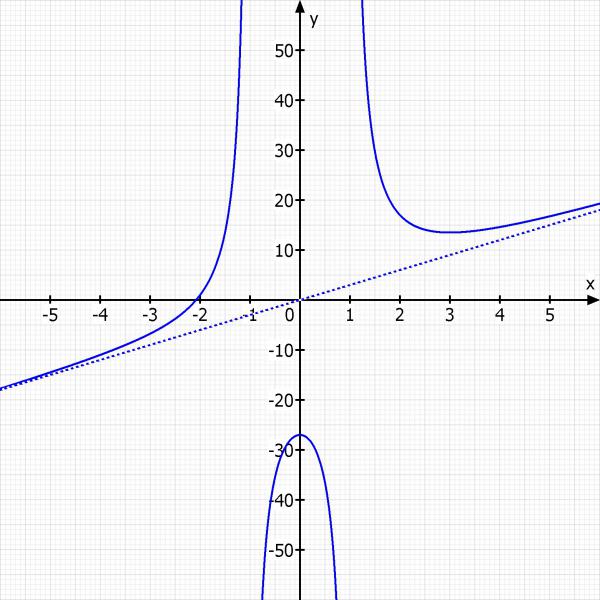
Skizze:

Comments

Ich danke dir erstmal für die ausführliche Antwort!

Ich hätte aber eine Frage zur Skizze welche Funktion ist wo eingezeichnet ?

Die Asymptote sieht man ja auf Anschlag jedoch wird mir nicht so ganz klar welche Werte in welche Funktion eingesetzt wurden um den rest zu Zeichnen.

---

Der Rest ist eine Funktion und nicht mehrere.

Sie erhältst du, indem du von 

f(x) = (3·x³ + 27)/(x² - 1)

eine Wertetabelle machst und die erhaltenen Punkte in ein Koordinatensystem einträgst.