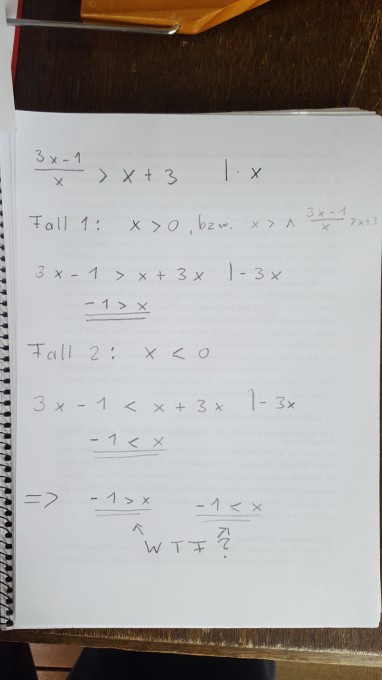Ich bin neu hier, aber hoffe, dass ihr mir helfen könnt. Ich beschäftige mich gerade mit Ungleichungen und komme etwas durcheinander, ich habe folgende Fragen,:
Wann darf man ein Vorzeichendiagramm verwenden, nur, wenn die Ungleichung < ; >; oder kleinergleich 0 sein soll?
Die zweite Frage handelt sich um die Lösung von rational gebrochenen Ungleichungen, wie bekannt, muss man dort eine Fallunterscheidung vornehmen, wenn man den Nenner eliminieren möchte. Wenn ich dies tue, erhalte ich jedoch nur widersprüchliche Ergebnisse (s Bsp unten) was mache ich falsch?
Bin jeder Antwort sehr dankbar.
!