Hallo Forenten,
ich habe hier zwei Aufgaben, welche sich beide mit Stichproben beschäftigen, jeweils aber unterschiedlich gelöst werden. Die Rechenwege selbst sind für mich verständlich, warum ich aber unterschiedliche Lösungsmechanismen heranziehen muss, leider nicht.
Es wäre schön, wenn mir hierbei hier jemand helfen könnte. :)
hier sind nun die Aufgabenstellungen, die Lösungsansätze habe ich abfotografiert:
Aufgabe 1)
Einem Golfmagazin zufolge ergibt sich auf einem bestimmten Golfplatz eine durchschnittliche Schlagzahl von 95. Zudem weist die Schlagzahl eine eine Standardabweichung von 14 auf. Behandeln Sie diese Werte als Werte der Grundgesamtheit. Der Betreiber erhebt nun eine Stichprobe von 30 Golfspielern. --> Wie hoch ist die Wahrscheinlichkeit dafür, dass das Stichprobenmittel der Golfer maximal 3 Schläge vom Wert der Grundgesamtheit abweicht?
Aufgabe 2)
Ein Produktionsprozess wird regelmäßig auf seine Qualität überprüft. Der zuständige Inspekteur nutzt dafür einfache Zufallsstichproben. Bei jeder Qualitätskontrolle wählt er zufällig n=30 Produkte und berechnet das durchschnittliche Gewicht der Stichprobe. [...] Annahme einer Normalverteilung und eines wahren Mittelwerts von 2kg. --> Berechnen Sie die Wahrscheinlichkeit, dass das durchschnittliche Gewicht der Produkte um 0.05kg vom wahren Mittelwert abweicht.
Die benutzten Formeln habe ich in grün dazu geschrieben.
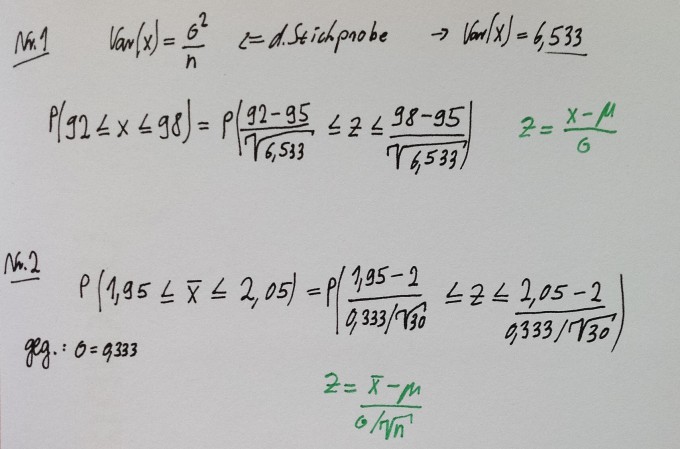
warum wird hier welche Formel benutzt, für mich sind irgendwie beide Aufgaben gleich :/
danke schonmal :)
