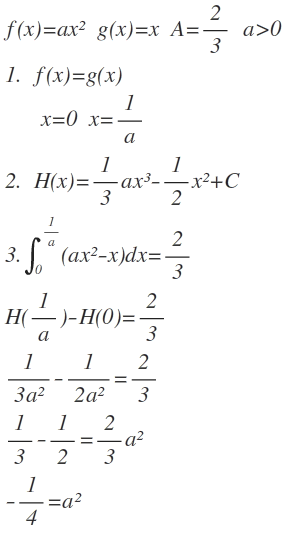Integralrechnung Erklärung gesucht

Question

Es geht um die Integralrechnung. Die Variable a soll ermittelt werden. Dies habe ich getan siehe Foto, am Ende kommt a=0,5 heraus. Wie man sieht, kann man von einer negativen Zahl keine Wurzel ziehen. Das heißt man muss den Betrag nehmen. Nun stellt sich die Frage, wieso man den Betrag nehmen muss?
Wenn man aber h(x)=g(x)-f(x) bestimmt, dann kommt man am Ende auf einen postivien Wert, von dem man die Wurzel ziehen kann. Wann kommt denn immer ein psotiver Wert heraus?

Ich brauche nun eine Begründung, wieso man den Betrag nehmen muss bzw. was man tuen muss, wenn man ein negativen Wert hat, von dem man die Wurzel ziehen muss.

Ich weiß, dass ich gerade selbst die Frage beantworte, dass man bei einem negativen Wert den Betrag nehmen muss, aber ich brauche eine andere "richtige" Erklärung.

Answer 1

da die Gerade im Intervall  ] 0 ; 1/a [ oberhalb der Parabel liegt,  subtrahierst du mit

∫ (ax² - x) dx  den größeren Flächeninhalt vom kleineren und erhältst ein negatives Ergebnis.

Deshalb muss man den Betrag setzen  A = | ∫ ... |

Gruß Wolfgang

Comments

Vielen Dank für die Antowort.

Dazu habe ich eine Frage:

Woher weißt, dass die Fläche oberhalb der Parabel ist?

Und, woran erkennst du, dass man kleine A. - größere A. rechnet.

Das ist mir nicht klar.

Vielen Dank nochmal

---

für x = 1/ (2a) ∈ ] 0 ;  1/2a [  ist a • x² = a • 1/(4a²) = 1/ (4a) < x 

Anschaulich kannst du auch für a= 1 die Gerade y=x und die Normalparabel einfach zeichnen.

> Und, woran erkennst du, dass man kleine A. - größere A. rechnet 

Muss man nicht, aber du hast so gerechnet.

Wenn "Größere A - kleinere A"  [ also ₀∫ ^1/a  (x - ax²)  dx   rechnet, benötigt man keinen Betrag. Schaden kann er aber nie, wenn man nicht weiß, welcher Graph oben liegt.

 

---

Eine kleine Frage habe ich noch:

Wenn ich die Grahen f(x)=0,5x² und g(x)=x zeichne und weiß dass der Flächeninhalt durch die Aufgabe 2/3 ist, kann man sagen, dass Die Fläche unter dem Graphen 2/3 beträgt und die Fläche unter der Gerade 4/3 ist?

Wie ich dazu komme:
Dort befindet ich ein rechwinkliges Dreieck also:
0,5*2*2=2

Da die untere fläche 2/3 ist ergibt sich 2-2/3=4/3 geht das?

Ich hoffe einer von euch kann noch antworten.

Vielen dank

---

Nein,

du weißt nur, dass die Differenz 2/3 ist:   5/6 - 1/6 = 4/6 ergibt z.B. ebenfalls 2/3

---

okay danke.

also kann man nicht sagen das fläche unter dem graphen größer ist als die unter der parabel?

Answer 2

Die Antwort ist sehr einfach. Du rechnest die Fläche unterhalb der Parabel minus die Fläche unterhalb der geraden aus. Die gerade liegt aber oberhalb der parabel, jedenfalls zwischen den Schnittpunkten. Wenn du eine  positive Fläche willst, stelle die Differenzflächenfunktion immer so auf, dass du mit der oben liegenden Kurve anfängst.

Comments

Jaa jetzt ist es mir klar. Dankeschön.

Für diese Erklärung benötigt eine Zeichnung oder um es klarzustellen oder?

---

Eine Kleine Frage habe ich:
Rechnet man normalerweise auch immer mit der Fläche unterhalb der Parabel und unterhalb der Geraden..?
Bildet das also die Differenzfunktion?

---

Ja genau man macht eine Zeichnung. Und ja um die Fläche zwischen den kurven rauszukriegen bildet man die differenzfunktion.

---

Eine kleine Frage habe ich noch:

Wenn ich die Grahen f(x)=0,5x² und g(x)=x zeichne und weiß dass der Flächeninhalt durch die Aufgabe 2/3 ist, kann man sagen, dass Die Fläche unter dem Graphen 2/3 beträgt und die Fläche unter der Gerade 4/3 ist?

Wie ich dazu komme:
Dort befindet ich ein rechwinkliges Dreieck also:
0,5*2*2=2

Da die untere fläche 2/3 ist ergibt sich 2-2/3=4/3 geht das?

Ich hoffe einer von euch kann noch antworten.

Vielen dank

---

Die Fläche zwischen den beiden Graphen beträgt 2/3. Dementsprechend beträgt die Fläche unter der Parabel 4/3.

---

Die fläache unter der gerade muss doch grösser sein als die der unter parabel oder?

Grsse fläche-kleine Fläche = positiv

---

Ja genau richtig.