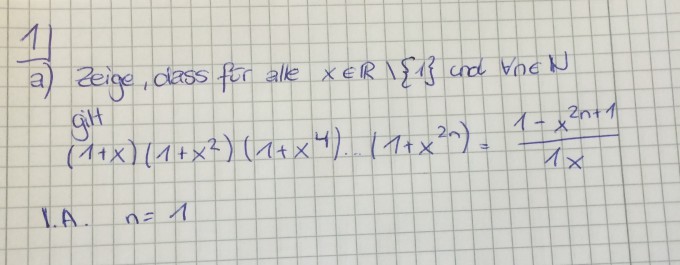vollständige induktion hilfe induktionsanfang

Question

hallo

hier soll man das mit vollständiger Induktion beweisen.

leider versteh ich nicht einmal die Aussage

angenommen n=1 dann steht rechts noch (1-x^3)(1-x)

und wenn man mal ausprobiert für x=2 kommt rechts 7 raus

bloß was muss man links multiplizieren, damit man aus 7 kommt?

oder was entspricht links n=1?

Answer 1

Deine Behauptung soll wohl heißen

(1+x)(1+x^2)(1+x^4)(1+x^8)....(1+x ^{2 hoch n})= ( 1 - x ^{2 hoch (n+1)} ) / ( 1 - x)

dann stimmt es nämlich auch für n=1

(1+x)(1+x^2) = ( 1 - x⁴) / (1 -x )

denn beides ist = 1 + x+ x^2 + x^3 .

Answer 2

 n=1 dann steht rechts noch (1-x³) / (1-x)  sollte da stehen, wenn du in der Behauptung ein Minus vergessen hast.

Was hast du denn links bei n=1? 

(1 + x)(1+x^2) ?

Bitte Behauptung nochmals kontrollieren. 

Comments

Schau mal, was WA bekommt, wenn man links mit dem (vermuteten) Nenner mutlipliziert: https://www.wolframalpha.com/input/?i=(1%2Bx)(1%2Bx%5E2)(1%2Bx%5E4)(1%2Bx%5E8)+(1-x)

---

Ja habe das Minus vergessen

Jedoch komme ich immer noch nicht auf den induktionsschritt