Steckbriefaufgabe: Parabel dritter Ordnung mit waagerechter Tangente in P(1/4) und W(0/2)

Question

Hilfeeeee.. wie soll ich das lösen?

Eine Parabel 3.Ordnung hat in P(1/4) eine waagerechte Tangente und in Q(0/2) ihren Wendepunkt ?

Answer 1

Hi,

allgemeine Form: y=ax³+bx²+cx+d

Ableitungen:

f'(x)=3ax²+2bx+c

f''(x)=6ax+2b

 

Bedingungen:

f(1)=4   (Punkt P)

f'(1)=0  (waagerechte Tangente)

f(0)=2   (Punkt Q)

f''(0)=0  (Wendepunkt)

 

Vier Bedingungen brauchts um die vier Unbekannten zu finden. Diese nun sauber aufgeschrieben:

a + b + c + d = 4
3a + 2b + c = 0
d = 2
2b = 0

 

Das gelöst und man erhält:

a=-1, b=0, c=3 und d=2

 

Also: f(x)=-x³+3x+2

 

Grüße

Comments

benötige ich bei einer Parabel dritter Ordnung nach cx noch das d???

---

Wie meinst du das jetzt? Im Resultat von Unknown ist cx+d doch schon berechnet als 3x+2.

f(x)=-x³+3x+2

Answer 2

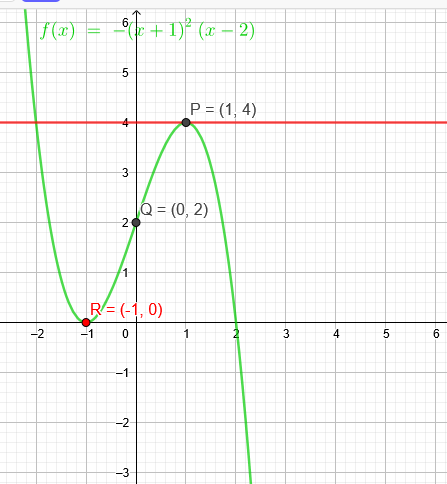
"Eine Parabel 3.Ordnung hat in P(1|4) eine waagerechte Tangente und in Q(0|2) ihren Wendepunkt ?"

Da eine Parabel punktsymmetrisch zum Wendepunkt liegt, muss sie in R(-1|0) auch eine waagerechte Tangente besitzen:

$f(x)=a*(x+1)^2*(x-N)$

P(1|4)

$f(1)=a*(1+1)^2*(1-N)=4a*(1-N)$

$4a*(1-N)=4$  →  $a=\frac{1}{1-N}$

$f(x)=\frac{1}{1-N}*[(x+1)^2*(x-N)]$

$f´(x)=\frac{1}{1-N}*[(2x+2)(x-N)+(x+1)^2]$

$f´(1)=\frac{1}{1-N}*[(2+2)(1-N)+(1+1)^2]$

$f´(1)=0$         $N=2$         $a=-1$

$f(x)=-(x+1)^2*(x-2)$