Hallo Chiciasena, lange nichts von dir gehört :-)
> Geben Sie jeweils die Gleichung
> - einer Polynomfunktion 4. Grades an
> symmetrisch zur y.Achse
→ die Funktionsgleichung hat nur gerade Hochzahlen bei den x-Potenzen:
f(x) = ax4 + bx2 + c (die Zahlen a,b und c müssen wir bestimmen:
> verläuft durch den Punkt S(0/3)
für x=0 hat man also den y-Wert 3
f(0) = 3 also : a • 0 + b • 0 + c = 3 → c = 3
→ f(x) = ax4 + bx2 + 3
> hat in T(3/0) einen Tiefpunkt.
f(3) = 0 also: a • 34 + b • 32 + 3 = 0
→ 81a + 9b + 3 = 0 | : 3 → 27a + 3b + 1 = 0 #
bei einem Tiefpunkt muss die Ableitung f '(x) den Wert 0 haben:
f '(x) = 4ax3 + 2bx
f '(3) = 4a • 33 + 2b• 3 = 0 → 108a + 6b = 0 →:6 18a + b = 0
→ b = -18a
b dort einsetzen: 27a - 3 • 18a = -1 → -27a = -1 → a = 1/27
# 27 • 1/27 + 3b = -1 → 1 + 3c = -1 → 3c = -2 → b = -2/3
Also: f(x) = 1/27 x4 - 2/3 x2 + 3
wenn man die Funktion zeichnet, sieht sie so aus:
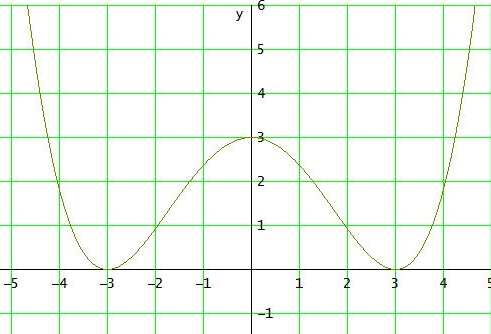
Gruß Wolfgang