Bestimme die fehlende Koodinate so, dass a -> b

Question

->

a=   1                          2

       a2   ,  b ->  =       -1

        3                           1

und

a=   -1                          3

       4   ,  b ->  =       -0

        2                          b3

ich versteh es leider gar nicht..

Comments

Sollen die drei Punkte jeweils auf einer Geraden liegen?

---

Falls ich dir weiterhelfen soll stelle einmal ein
Foto ein. So sagen mir die Angaben nichts.

mfg Georg

---

Mein Tipp  :   a2=5 ; b3=1,5

Answer 1

Bestimme die fehlende Koodinate so, dass \(\overrightarrow{a}\perp\overrightarrow{b}\).

$$ \overrightarrow{a} = \begin{pmatrix} 1\\a_2\\3 \end{pmatrix}, \quad \overrightarrow{b} = \begin{pmatrix} 2\\-1\\1 \end{pmatrix}$$Ein wenig Kopfrechnen führt zu

$$ \overrightarrow{a}\perp\overrightarrow{b}\quad\Leftrightarrow\quad a_2=5.$$Sieh zu, dass das Skalarprodukt \(\overrightarrow{a}\cdot\overrightarrow{b}=0\) wird.

Answer 2

Nr. 1

Ich denke mal, die drei Punkte sollen auf einer Gerade liegen:

Du kannst die beiden gegebenen Punkte und die zugehörige Gerade in ein Koordinatensystem einzeichnen, und beim dritten Punkt die fehlende Koordinaten ablesen. Wenn du rechnen musst, kannst du bei dieser Zeichnung den 2. Strahlensatz anwenden. Wenn du den noch nicht kennst, geht es auch so:

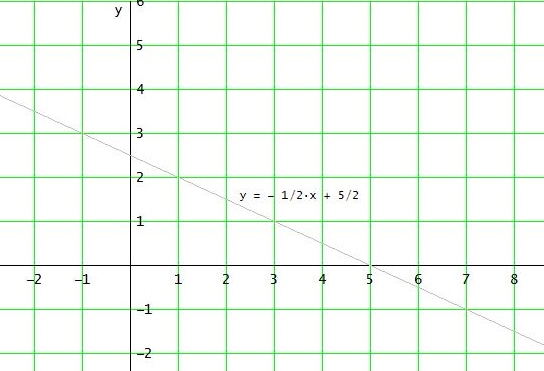
Die Gerade durch (-1|3) und (3|1) hat die Steigung m = (1 - 3) / (3 - (-1)) = - 1/2

Die Gerade durch den Punkt P( x_p | y_p ) mit der Steigung m hat die Gleichung

y = m • ( x - x_p ) + y_p            [ Punkt-Steigungs-Formel ]   

→  y = -1/2 • ( x + 1 ) + 3 = -1/2 x + 5/2

mit x = a₂  und   y = b₂ = -1  ergibt sich  -1 = -1/2 a₂ + 5/2  → a₂ = 7

Die zweite solltest du mal allein versuchen!

[ Kontrolllösung: b₃ = 6/5 ]

Gruß Wolfgang