Statistikaufgabe über Sportergebnisse

Question

folgende Statistikaufgabe ist gegeben:

Lösungen:


Hinweis: Wir sollen die Werte nicht runden! Normalerweise rundet man die Werte mit maximal 2 Stellen hinter dem Komma, z.B. 2.568≈2.57. Also nicht über die vielen Stellen nach dem Komma wundern (Außnahme: Funktion g(x)).
⇓


(d) Betrachtet man den Korrelationskoeffizient (r_xy): -0.90 und die lineare Regression: -0.80x+17.26 könnte man meinen, dass beide miteinander zusammenhängen. Dennoch werden bei der linearen Regression nicht die x-Fehler betrachtet.

Bei (d) bin ich mir nicht so sicher. Ansonsten wie immer überprüfen, ob alles richtig ist.

Beste Grüße

Comments

 f(x) = -0,803925 * x + 17,256265

Die Regressionsgerade stimmt also schon einmal.

oben angegebenen Formel den Korrelatiosnkoeffizenten

Die Angabe der Formel fehlt.

mfg Georg

---

Hallo Georg,

es ist die Formel unter dem Mittelwert von y (r:=...). Die Formel stand unten auf der Rückseite des Blattes und ich habe es vergessen oben in der Aufgabenstellung oberhalb einzufügen. Wie könnte man die Teilaufgabe (d) argumentativ lösen?

---

Unglücklichsterweise kenne ich mich mit Korrelationskoeffizienten
nicht aus. Ich werde mich einmal per Internet kundig machen

Ich will jetzt aber erst einmal fernsehen.

mfg Georg

Answer 1

Hallo Asterix,

Videolink
https://www.youtube.com/watch?v=z7Ldw5an0Q0

r = -0.9

Das minus bedeutet : der Trend ( Steigung der Regressionsgerade ) ist fallend.
0.9 bedeutet : die Streuung der Werte um die Regressionsgerade ist gering.
Die Gerade passt gut.

| r | ( absolut ) r  zwischen 0 und 1
0 große Streuung der Werte ( Sternenhimmel )
1 : liegen perfekt auf der Geraden.

siehe deinen 1.Plot

Comments

Hallo Georg,

das Video ist einwandfrei, vielen Dank dafür! Das Video hat alles wunderbar beschrieben. Also besteht doch ein Zusammenhang aus errechneten Korrelationskoeffizienten r=-0.9 und der Regressionsgerade im Scatterplot. Die Streuung ist in der Tat gering und man sieht den Abwärtstrend (negative Steigung).

Beste Grüße

Asterix

---

Hallo Asterix,

ich bin allerdings auf einen logischen Widerspruch gestoßen

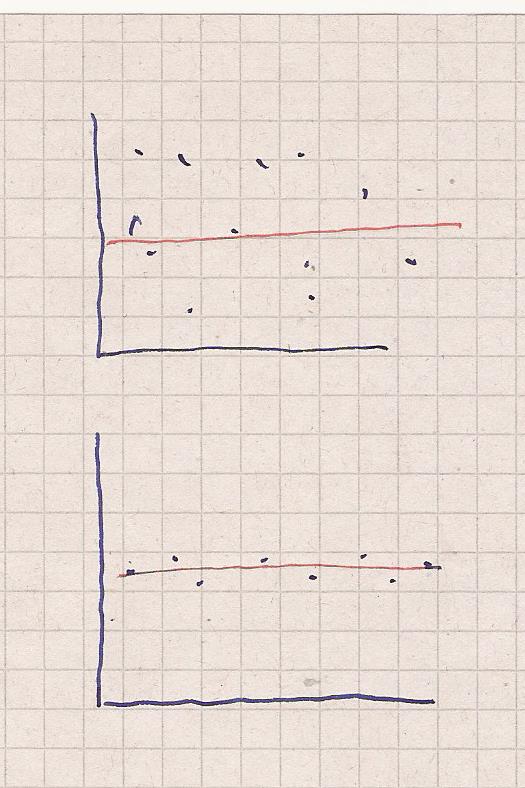
Sowohl im Sternenhimmel als auch bei den näherliegenden Punkten in Bild 2
sei die Steigung der Regressionsgeraden 0.

Dann müßte der Korrelationskoeffizent ja 0 sein, weil weder steigend noch fallend.

Andererseits hat der Sternenhimmel weit mehr Streuung ( angenommen 0.1 )
als Bild 2 ( angenommen 0.9 )

Was wäre den jetzt der Korrelationskoeffizent für die beiden Bilder ?

---

Ich denke, dass alle Punkte eine Art Gerade ergeben müssten (x x x x x), damit r=0 ist bzw. eine sehr hohe Korrelation erfüllt ist sowie ein horizontaler Trend erkennbar ist. Nun zu Deiner Frage:
Auf dieser Website denke ich, ist es gut beschrieben:

 http://www.uni-stuttgart.de/soz/avps/mitarbeiter/Jakob/WWW/SPSS/Korrelation.html 

Horizontaler Trend durch Datenpunkte im Scatterplot (vergleichbar mit f(x)=2 u.a).

Bild 1: hat eine sehr geringe Korrelation (≤±0.20)
Bild 2: hat eine hohe bzw. sehr hohe Korrelation (≥±0.9)

Answer 2

Ein kleiner Tipp noch, die Berechnung des Korrelationskoeffizienten ist mit der folgenden Formel einfacher, als die, die du oben verwendet hast. Man ist schneller und auch die Gefahr von Rundungsfehlern ist viel geringer:

In diesem Video wird einfach erklärt, wie man die Formel verwenden kann um den Korrelationskoeffizienten einfach zu berechnen. Außerdem gibts noch viele Infos über die Interpretation und worauf man sonst noch so achten muss.
https://youtu.be/t8lfC_68MB4