Grenzwert berechnen Bruch Logarithmus. f(x) = ln(1-x)/(1-x)

Question

kann mir jemand zeigen, wie ich folgenden Grenzwert berechne?

Soll für diese Funktion eine Kurvendiskussion machen und hänge an diesem Punkt. Den Definitionsbleich habe ich vorher eingeschränkt:

D(f)= (-∞ , 0]

Kann ja hier kein x ausklammern und Regel von l'Hospital funktioniert auch nicht.

Danke für die Hilfe im Voraus!

Answer 1

Warum hast du z.B. 0.5 aus dem Definitionsbereich ausgeschlossen ?

lim (x --> -∞) LN(1 - x) / (1 - x)

Subst. z = 1 - x

lim (z --> ∞) LN(z) / z

L'Hospital

lim (z --> ∞) (1 / z) / 1 = 0

Comments

stimmt, Definitionsbleich muss natürlich lauten D(f)= (-∞ , 1).

Also doch mit l'Hospital.

---

Noch eine Frage dazu:

Wenn ich substituiere und dann sehe, dass mein z --> 0 geht, woher weiß ich dann, dass dann auch mein x --> 0 geht?

Habe jetzt mal die "rechte Grenze = 1" in den substituierten Ausdruck eingesetzt und dann kommt 1 raus.

Die Funktion geht doch aber hier gegen minus unendlich.

---

x geht gegen 1-h.

z geht dann gegen 1 - x also 1 - (1-h) also 0+h.

lim (z --> ∞) LN(z) / z = - ∞ / 0+ = - ∞

---

glaube das ist das, was mir gerade Probleme bereitet.

was bedeutet jetzt hier das h?

Kann das gerade nicht wirklich nachvollziehen :/

---

Das h ist eine infinitisimal kleine Größe. Ich wollte zuerst nur 1^- schreiben. Das schreibt man normalerweise. Ich habe mich dann aber für das 1 - h entschieden um dir klarer zu machen gegen welchen Wert die Unbekannten laufen.

Answer 2

für x-> 0 brauchst du nur x= 0 einzusetzen.

Zähler ln(1-0) = ln(1) = 0

Nenner (1-0) = 0

Zähler/Nenner = 0/1 = 0. Fertig.

Sowohl h(x) = ln(1-x) als auch g(x) = 1-x sind in x=0 stetig. Vgl.

 ~plot~ ln(1-x); 1-x ~plot~ 

Comments

ok, das heisst ich kann immer substituieren und der Grenzwert bleibt der gleiche?

Und wie komme ich nun auf die -∞ wenn ich x -->1 laufen lasse?

---

für x->0 brauchst du nicht zu substituieren. Vgl. meine Rechnung.

Für x-> 1 ist eine Substitution sinnvoll.

limes ln(1-x)/(1-x)      für x gegen 1-   (von links)  | Subst. z = 1-x

= limes ln(z)/z        für z gegen 1+ (von rechts) | vielleicht Subst. u = ln(z)

= limes u/e^{u}     für u gegen "Was denkst du?"

~plot~ ln(x); e^x ~plot~ 

---

...

Für x-> 1 ist eine Substitution sinnvoll.

limes ln(1-x)/(1-x)      für x gegen 1-   (von links)  | Subst. z = 1-x

...

so weit bin ich und GENAU da liegt mein problem.


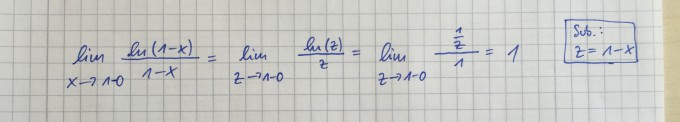
warum gehst du dann von einmal von rechts an die 1, nachdem du substituiert hast. Und dann nochmal mit u substituieren? Das verwirrt mich komplett.
Gibt es nicht eine einfache Möglichkeit mein Aufgeschriebenes zur Lösung zu bringen?
Sorry, komme gerade nicht darauf.

---

Du brauchst eigentlich überhaupt nicht substituieren, wenn dich das verwirrt. Ich habe es gemacht, damit der Ausdruck für dich einfacher ist. Du kannst u = ln(z) substituieren, wenn du mit dem Grenzwert von e^u besser klar kommst als mit ln(z).

Beide Substitutionen sind aber nicht notwendig. Es geht auch ganz ohne.

---

"Beide Substitutionen sind aber nicht notwendig. Es geht auch ganz ohne."

ok, das war das Stichwort :D 

Jetzt komme ich auf das Ergebnis.