Ortskurven berechnet man z.b. bei Kurvenscharen
Z.B.
ft(x) = x^2 + tx + t
Uns interessiert hier z.B. die Ortskurve aller Hochpunkte. Also eine Funktion auf der ich alle Tiefpunkte finde.
Dazu berechne ich erst mal den Tiefpunkt
ft'(x) = 0
2x + t = 0
x = -t/2
Damit wüßte ich dann die x-Koordinate meines Tiefpunktes. Das interessiert mich aber jetzt nicht, sondern ich will lieber gleich wissen, wie mein t sein muss, damit ich bei x einen Tiefpunkt habe. Damit löse ich die Bedingung nach t auf.
2x + t = 0
t = -2x
Wenn ich das jetzt in die Ursprungsfunktion einsetze erhalte ich die Ortskurve aller Tiefpunkte.
f(-2x) = x^2 + tx + t = x^2 + (-2x)x + (-2x) = x^2 - 2x^2 - 2x = - x^2 - 2x
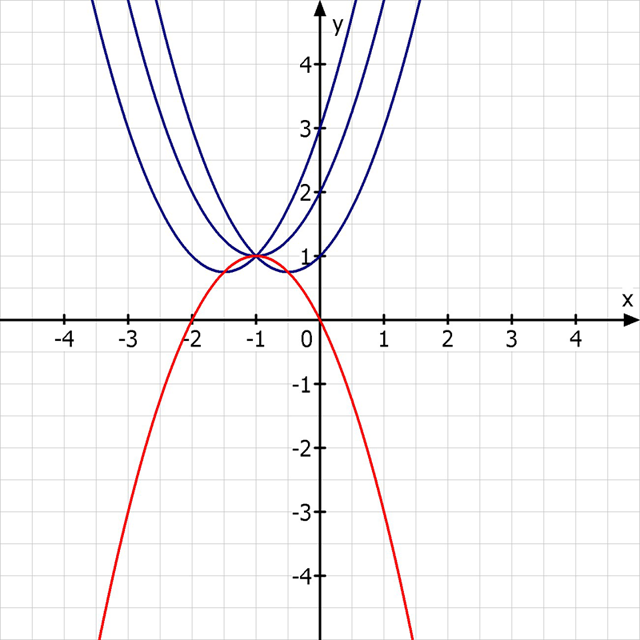
Das sollte die Ortskurve der Tiefpunkte sein.
Ich Zeichne jetzt mal die Funktion für t=1, 2 und 3 und die Ortskurve