Elementargeometrie mit eingerostetem Zirkel, der nur noch den Radius 3cm hat.

Question

Joes Zirkel ist eingerostet und kann nur Kreise mit dem Radius 3cm zeichnen. Sein Lineal ist zum Glück noch ganz. Gegeben sein eine mehr als 3 cm lange Strecke AB und eine Gerade l, welche nicht die Punkte A und B enthält. Der Abstand von A zu l sei kleiner als die Länge von AB. Wie kann Joe den Schnittpunkt von l mit Kreis um A durch B konstruieren?

Comments

Überlege dir zunächst, wie man eine Parallele zu einer gegebenen Geraden durch einen gegebenen Punkt konstruieren kann. Der Rest ist Strahlensatz (zentrische Streckung).

---

Zum Punkt A meinst du dann?

---

Hi, ich habe eine Aufgabe mit der ich nicht klar komme. Kann mir wer bitte die Konstruktionsanleitung dafür geben? Die Aufgabe lautet wie folgt:

---

Der Winkel α = BAC ist gegeben und kann mit dem Zirkel halbiert werden. Wähle einen Punkt P im Abstand 3 cm von A und schlage den Thaleskreis um P. Dieser schneidet die Winkelhalbierende in Q und AB in R. Eine Parallele zu QR durch B schneidet AC in D.

---

Das ist weder für die andere noch für diese Frage eine geeignete Konstruktion.

---

Das ist ein Kommentar zum Kommentar von hj2111

Hier mal eine Skizze zum Ziel dieser Konstruktion:

Vorschlag von Gast hj2111 gibt bei mir folgende Planfigur:

 

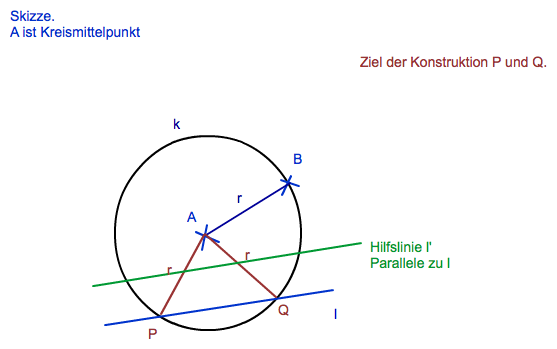
Plan: Konstruiere erst eine Parallele l' zu l, die so nahe bei A liegt, dass dein Zirkel gerade passt. Dann die Figur noch strecken. 

Nur: Wie genau kommt man zum richtigen Abstand von A, wenn man den Zentriwinkel nicht kennt?  

---

Es funktioniert folgendermaßen :

---

Hj2111, 

Kannst du bitten eine Anleitung kurz schreiben? Ich verstehe nix. Bitte Bitte.

---

Mache zuerst eine zentrische Streckung mit Zentrum A, die B auf den Kreis um A abbildet. Dabei wird gleichzeitig die Gerade l auf l' abgebildet. Die Schnittpunkte von l' mit dem Kreis werden anschließend zurückgestreckt.

---

Korrektur :  Der Strich gehört in den Zähler.

---

Welcher Strich? 

Habe bei Wiki gegooglt was eine zentrische Streckung ist. Versteche ich leider nicht. Kannst du erst mal nur ein Bild machen mit nur einer Strekung und dann Stück für Stück weiter machen wenn ich es verstanden habe? 

---

Welcher Strich?

Statt  f = AB / AB'  muss es heißen  f = AB' / AB .
Mein Text im darauf folgenden Kommentar ist richtig.

Den Rest erklärt dir sicher gern jemand anders.

---

Also l(Strich) und S1(Strich) bekomme ich schon hin. Wie bekommen ich P?

---

Du wähst P beliebig auf deiner Gerade. Dann kannst du P' bestimmen , weil AP'/AP=f. Jetzt kannst du auch l' konstruieren.

---

Man sollte am besten P so wählten, dass du die Strecke AP im Verhältnis AP'/AP=AB'/AB=f aufteilen kannst. Dann nimmst die 3 cm als Einheitslänge und konstruiertst P'.

Answer 1

Der Winkel α = BAC ist gegeben und kann mit dem Zirkel halbiert werden. Wähle einen Punkt P im Abstand 3 cm von A und schlage den Thaleskreis um P. Dieser schneidet die Winkelhalbierende in Q und AB in R. Eine Parallele zu QR durch B schneidet AC in D.

Comments

Das verstehe ich noch nicht ganz. Also Der Winkel Alpha ist klar. Und ich kann auch die Winkel halbierende konstruieren. Dazu ziehe ich einen Kreis um A mit 3cm. Dieser schneidet einmal die Strecke AB und einmal AC. In beiden Schnittpunkten setze ich wieder den Zirkel an und ziehe wieder zwei Kreise mit 3cm Radius. Einmal schneiden Sie sich in A und noch ein weiterer Schnittpunkt W1 (siehe Skizze1) und schon habe ich die Winkelhalbierende. Danach habe ich einen Kreis um A gezogen mit r=3cm. habe mir den Punkt P gesucht (siehe Skizze2) Habe mir einen Punkt auf dem Kreis gesucht und wieder einen Kreis mit r=3cm gezogen. Dieser schneidet A die Strecke AB und die Winkelhalbierende. Ich weiß nicht was du mit Q und R meinst? 

---

Ich habe vergessen, zu erwähnen, dass P auf AB liegen soll.

---

Und P soll 3cm von A entfernt sein? 

---

Ja, alles andere bleibt so. Inzwischen stelle ich fest, dass es noch einfacher geht.

---

Wie? Kannst du es mir sagen? 

---

Zeichne die Strecken AB und AC. Schlage mit dem eingerosteten Zirkel eine Kreis um A. Dieser Schneidet AB in E und AC in F. Die Parallele zu EF durch B schneidet AC in D. Die Konstruktion einer solchen Parallelen erfordert eine zusätzliche Konstruktion.