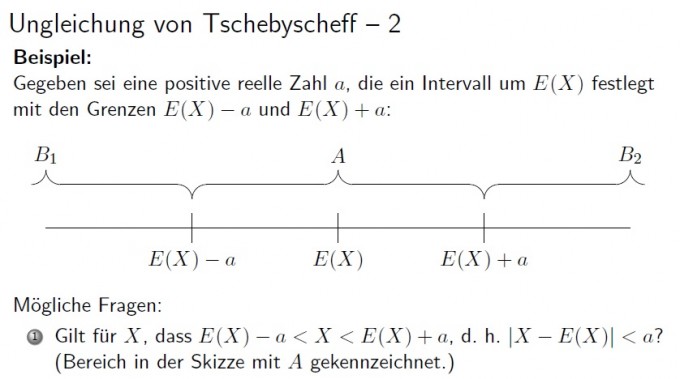
Wir sind uns doch einig, dass die gesuchte Wahrscheinlichkeit in der Verteilung bei X=10 (5% der 200 Bauteile) liegen soll... laut meinen Unterlagen hier ist das a (du hast es k genannt) also die Differenz von der gewünschten Stelle und der des Erwartungswert... also kann a doch nicht 10 sein!..oder bin ich jetzt völlig neben der Spur? Dann erkläre mir bitte anhand dem Foto, dass ich hochgeladen habe, warum ich nicht Recht habe...
(Meine Formel mit dem EW^2 habe ich übrigens im Kommentar zu meiner Frage schon korrigiert)