zunächst sollst Du in jedem der 6 Bildchen die Vektoren beschriften. Ich habe das mal für Dich gemacht und jedes Bild mit einer Nummer versehen, so das klar ist, was ich mit was meine.
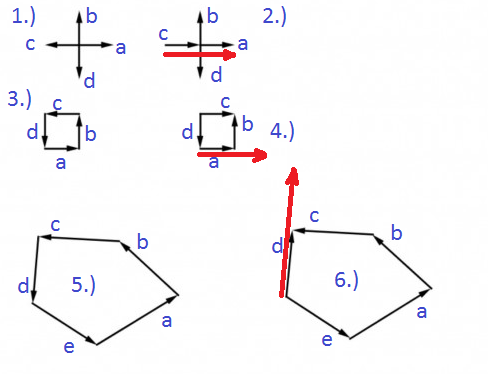
a) zu den Ergebnisvektoren: bei den Bildern 1, 3 und 5 ist die Summe aller Vektoren stets der Nullvektor.
Bei 2.) kann man davon ausgehen, dass \(a+b+d-c=0\) ist. Addiere ich \(2c\) auf beiden Seiten, so erhält man \(a+b+c+d=2c\). Entsprechendes gilt bei 4.). Hier ist \(a+b-c+d=0\) also ist die Summe aller vier Vektoren wieder \(2c\). Bei Bild 6.) wiederholt sich das ganze zum dritten Mal. Hier gilt \(a+b+c-d+e=0\) die Addition mit \(2d\) ergibt dann die Summe aller 5 Vektoren.
b) Die Gemeinsamkeit ist bei 1, 3 und 5, dass die Vektorsumme =0 ist und bei den restlichen Bildern zeigt jeweils einer der Vektoren in die Gegenrichtung, was dazu führt, dass die Summe immer gleich zwei mal eben dieser Vektor ist.
Die Reihenfolge der Addition kann beliebig verändert werden, ohne dass sich das Ergebnis ändert. Probiere es einfach bei dem einen oder anderen Bild aus.
c) keinen! Die Beschriftung kann beliebig verändert werden. Es hat keinen Einfluss auf das Ergebnis.
Gruß Werner