Öltank mit zylindrischer Form: Fassungsvermögen abschätzen. Modellieren Sie das Bodenstück durch eine Wurzelfunktion.

Question

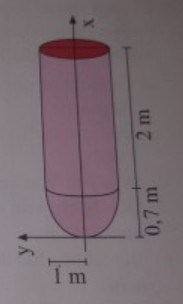
Ein Öltank hat die abgebildete zylindrische Form mit kuppelartigem Boden. Die Maße können der Zeichnung entnommen werden.

a) Schätzen Sie das Fassungsvermögen des Tanks grob ab, indem Sie ihn durch einen Zylinder gleichen Durchmessers ersetzen, der eine geeignet gewählte Höhe besitzt.

b) Modellieren Sie das Bodenstück durch eine Wurzelfunktion der Form \( f(x)=a \sqrt{x} \). Die Lage des Koordinatensystems können Sie der Abbildung entnehmen.

c) Bestimmen Sie nun das Fassungsvermögen des Bodenteils mit der Rotationsformel. Welches Gesamtvolumen hat der Tank?

d) In den Behälter fließen beim Befüllen 2 Liter Öl pro Sekunde ein. Nach welcher Zeit ist der Tank bis zur halben Höhe gefüllt?

e) Zur Reinigung des Tanks wird das Bodenteil bis zur Hälfte seines Fassungsvermögens mit dem Spülmittel gefüllt. Wie hoch steht das Spülmittel über dem tiefsten Punkt?

Answer 1

a)

pi * 1^2 * 2 < V < pi * 1^2 * 2.7

Es langt hier auch eine Abschätzung mit

V < pi * 1^2 * 2.7

b)

y = a·√x

x und y einsetzen und nach a auflösen

1 = a·√0.7

c)

∫ (0 bis 0.7) (pi·(√(10/7)·√x)^2) dx = ...

Rest sollte klar sein denke ich.

Comments

Vielleicht kannst du noch kurz die Ansätze zu d) und e) zeigen,

---

d)

Wie viel Liter gehen bis zur halben Höhe rein ?

Wie lange braucht es demnach wenn 2 Liter pro Sekunde in den Behälter fließen?

e)

Wie viel Liter gehen ins Bodenteil. Bis wohin ist es gefüllt wenn nur die Hälfte drin ist?

Hier bitte wieder mit dem Integral arbeiten.

---

Geht das?

d)

\( \pi \int \limits_{0}^{1,035}\left(\sqrt{\frac{10}{7}} * \sqrt{x}\right)^{2} d x= \)

e)

\( \pi^{*} \int \limits_{0}^{0,7}\left(\sqrt{\frac{10}{7}} * \sqrt{x}\right)^{2} d x+\pi^{*} 0,65 \)

---

d)

erstmal sicher nicht 1.035 sondern wenn 1.35. Aber auch 1.35 sind hier verkehrt.

Warum darfst du bis 1.35 mit absoluter Sicherheit nicht integrieren?

e)

auch hier hast du mit sicherheit nicht die aufgabe richtig verstanden. es geht nur um das Bodenteil.

Dafür sieht das was du hier als integral fabriziert hast schon recht gut für aufgabenteil d) aus.