Das zu maximierende Volumen ist $$V=h\left(\frac{d}{2}\right)^2 \pi$$
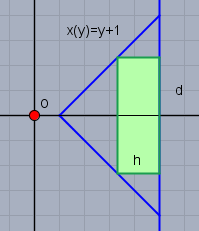
die Nebenbedingung lautet
$$h=5-x\left( \frac{d}{2} \right)=5-\left( \frac{d}{2}+1 \right)=4- \frac{d}{2} \quad \Rightarrow h +\frac{d}{2} -4 = 0 $$
Daraus folgt die Lagrange-Funktion
$$L(d,h,\lambda)= h\left(\frac{d}{2}\right)^2 \pi + \lambda \left( h +\frac{d}{2} -4 \right)$$
mit ihren Ableitungen
$$\frac{\delta L}{ \delta d}= h\frac{d}{2} \pi + \frac{1}{2} \lambda = 0$$
$$\frac{\delta L}{ \delta h}=\left(\frac{d}{2}\right)^2 \pi + \lambda = 0$$
aus der zweiten Gleichung folgt \(\lambda=-\left(\frac{d}{2}\right)^2 \pi\). Einsetzen in die erste
$$h\frac{d}{2} \pi - \frac{1}{2}\left(\frac{d}{2}\right)^2 \pi = 0$$
$$4h - d = 0 \quad \Rightarrow h=\frac{d}{4}$$
Einsetzen in die Nebenbedingung
$$\frac{d}{4} +\frac{d}{2} -4 = 0$$
$$\Rightarrow d=\frac{16}{3} \text{cm}$$
$$V=\frac{4 \text{cm}}{3}\left(\frac{16 \text{cm}}{6}\right)^2 \pi \approx 29,79 \text{cm}^3$$
Gruß Werner