Hi,
es lässt sich hier keine allgemeine Aussage für x->0 machen, da kein beidseitiger Grenzwert existiert.
Nichtsdestotrotz kann man damit beginnen, zweifach den l'Hospital anzuwenden. Man kommt dann auf
limx->0^{±} (e^{-x}+1)/6x = lim e^{-x}/6x+1/6x
Für x->0^+
e-Funktion wird 1 (da e^0=1) -> Zwei Summanden die jeweils nach ∞ streben, also auch insgesamt.
Für x->0^-
Genau das gleiche nur, dass wir hier beide Male nach -∞ streben, also auch insgesamt.
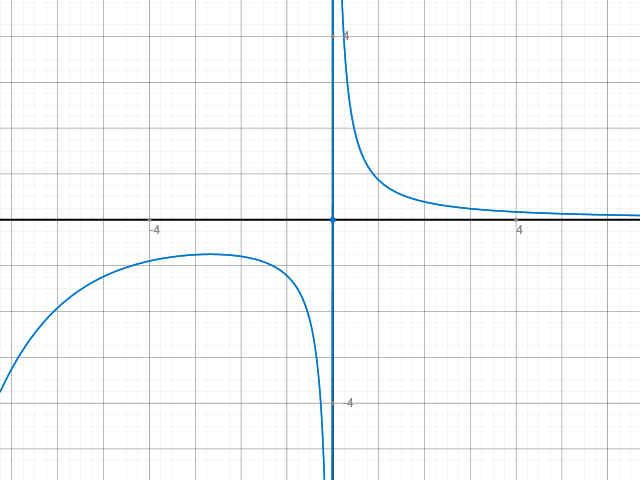
Auch zu sehen im Schaubild:
Grüße