Wie muss x gewählt werden, damit eine Schachtel mit maximalem Volumen entsteht?

Question

ich brauche hilfe bei folgender Aufgabe:

Aus einem quadratischen stück blech der seitenlänge 16cm werden an den ecken quadrate der seitenlänge x ausgestanzt, so dass aus dem restlichen blech eine nach oben offene blechschachtel gebogen werden kann. Wie muss x gewählt werden, damit eine Schachtel mit maximalem volumen entsteht?

Daanke :)

Answer 1

es liegt folgende Situation vor:

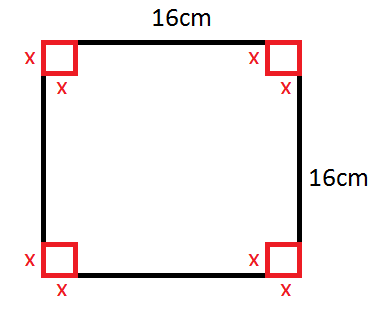
Die Höhe der Schachtel ist \(x\). Die Seitenlängen der Grundfläche sind jeweils \(16-2x\). Insgesamt ergibt sich für die Volumenfunktion in Abhängigkeit von \(x\): $$V(x)=x\cdot(16-2x)^2$$ Nun bildest Du die erste Ableitung, setzt diese gleich 0 und berechnest den Wert für \(x\): $$V'(x)=(16-2x)^2 - 4x\cdot(16-2x)=4 (64 - 32 x + 3 x^2)$$ $$V'(x)=0$$ Es gibt insgesamt 2 Werte für x, nämlich $$x_1=8$$ $$x_2=\dfrac{8}{3}$$ Weiterhin gilt: $$V(x_1)=V(8)=8\cdot(16-2\cdot 8)^2=0$$ $$V(x_2)=V(\dfrac{8}{3})=4\cdot(16-2\cdot \dfrac{8}{3})^2=\dfrac{4096}{9}$$ Für das maximale Volumen wählen wir also \(x=\dfrac{8}{3}\).

Konnte ich Dir damit weiterhelfen? Melde Dich bei Rückfragen gerne wieder!

André, savest8

Answer 2

Die Blechschachtel hat dann die Höhe x und die Grundkante (16-2x) und damit das Volumen v(x)= (16-2x)²·x. Nullstellen der Ableitung in v(x) einsetzen. Das x mit dem größeren Wert ist gesucht.