theq,
ich habe folgenden Gedankengang ... zunächst wandle ich die Binärzahlen (?) in Dezimalzahlen um und erhalte:
$$1_{(2)}=1_{(10)}$$ $$1000_{(2)}=8_{(10)}$$ $$1010001_{(2)}=81_{(10)}$$ $$10000000000_{(2)}=1024_{(10)}$$ $$11110100001001_{(2)}=15625_{(10)}$$ Dabei fällt (mit etwas Rumprobieren) auf:
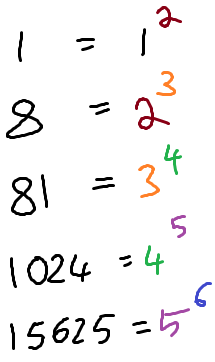
Aufgrund dieses Ergebnisses würde ich als nächstes \(6^7\) und \(7^8\) wählen. Die entsprechende Binärdarstellungen wären dann die nächsten beiden Folgeglieder, also
$$6^7_{(10)}=1000100010110000000_{(2)}$$ $$7^8_{(10)}=10101111111011011000001_{(2)}$$
Ob das nun die intendierte Lösung ist, kann ich nicht garantieren. Im Prinzip findest Du für zwei beliebige Folgenglieder auch immer ein Interpolationspolynom, auf dem dann alle Deine Folgenglieder liegen ... deshalb empfinde ich diesen Aufgabentypus immer etwas zu ergebnisoffen und ungeeignet für z.B. eine Analysis-Prüfung.
Ich hoffe, dass ich Dir damit ein wenig weiterhelfen konnte.
André, savest8