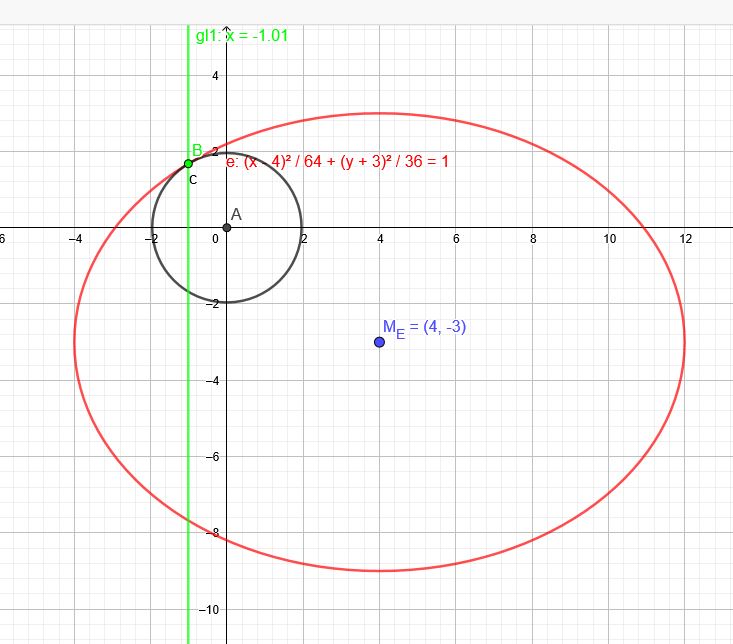
\(\frac{(x-4)^2}{64}+\frac{(y+3)^2}{36}=1\) →\(e(x,y)=\frac{(x-4)^2}{64}+\frac{(y+3)^2}{36}-1\)
\(e_x(x,y)=\frac{x-4}{32}\)
\(e_y(x,y)=\frac{y+3}{18}\)
implizites Differenzieren:
\(e'(x)=-\frac{\frac{x-4}{32}}{\frac{y+3}{18}}=-\frac{9(x-4)}{16(y+3)}\)
Mittelpunktskreis (Ursprung)
\(x^2+y^2=r^2\) → \(k(x,y)=x^2+y^2-r^2\)
\(k_x(x,y)=2x\)
\(k_y(x,y)=2y\)
\(k'(x)=-\frac{2x}{2y}=-\frac{x}{y}\)
Die Steigung im gemeinsamen Berührpunkt von Ellipse und Kreis ist gleich.
\(\frac{9(x-4)}{16(y+3)}=\frac{x}{y}\)
\(y=-\frac{48x}{7x+36}\) Schnitt mit Ellipse:
\(\frac{(x-4)^2}{64}+\frac{(-\frac{48x}{7x+36}+3)^2}{36}=1\)
\(x≈-1,011\) \(\frac{(-1,011-4)^2}{64}+\frac{(y+3)^2}{36}=1\) \(y≈1,68\)