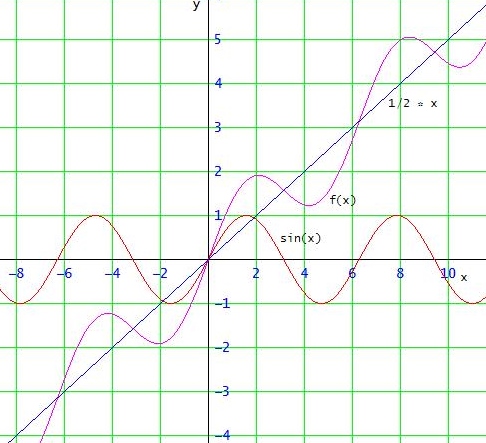
f(x) = 1/2 x + sin(x)
a)
sin(0) = sin(π) = sin(2π) = 0
→ f(0) = 0 ; f(π) = π/2 ; f(2π) = π
> Was lässt sich über Nullstellen von f aussagen?
In ] 0 , π [ addieren sich positive Werte zu f(x) → keine Nullstellen
f(π) = π/2 > 1 und 1/2 x ist streng monoton steigend
→ negative Sinuswerte ( ≥ -1 !) können 1/2 x in ] 0 , ∞ [ nicht ausgleichen
→ keine positiven Nullstellen.
analog in ] - ∞ , 0 [
→ f hat nur die Nullstelle x = 0
b)
Eine Funktion f ist am steilsten, wenn f " (x) = 0 ist:
f '(x) = COS(x) + 1/2
f "(x) = - sin(x) = 0 → x1 = 0 ; x2 = π ; x3 = 2π (Stellen, wo Gf am steilsten ist)
c)
Eine Stammfunktion von einer Funktion f ist nicht eindeutig bestimmt.
∫ (1/2·x + sin(x)) dx = 1/4·x2 - COS(x) + C
Eine Stammfunktion von f ist also
F : [0 , 2π ] → ℝ , F(x) = 1/4·x2 - COS(x) (mit C = 0)
Gruß Wolfgang